题目内容

函数f(x)＝ax2＋ax－1在R上恒满足f(x)<0，则a的取值范围是(　　)
A．a≤0B．a<－4
C．－4<a<0D．－4<a≤0
D
当a＝0时，f(x)＝－1在R上恒有f(x)<0；
当a≠0时，∵f(x)在R上恒有f(x)<0，
∴，∴－4<a<0.
综上可知：－4<a≤0.
练习册系列答案
相关题目
已知函数f（x）=1+
x-|x|
4

（Ⅰ）用分段函数的形式表示函数f（x）；
（Ⅱ）在坐标系中画出函数f（x）的图象；
（Ⅲ）在同一坐标系中，再画出函数g（x）=
1
x
(x＞0)的图象（不用列表），观察图象直接写出当x＞0时，不等式f（x）＞
1
x
的解集．
设f（x）是定义在R上的函数，且对任意实数x，恒有f（x+2）=-3f（x）．当x∈[0，2]时，f（x）=2x-x2．则f（0）+f（-1）+f（-1）+…+f（-2014）=（　　）
A．-
3
4
（1-31007）		B．-
3
4
（1+31007）
C．-
1
4
（1-
1
31007
）		D．-
1
4
（1+
1
31007
）
已知若的定义域和值域都是，则       ．
“a＝1”是“函数f(x)＝x2－4ax＋3在区间[2，＋∞)上为增函数”的________条件．
（2013•重庆）关于x的不等式x2﹣2ax﹣8a2＜0（a＞0）的解集为（x1，x2），且：x2﹣x1=15，则a=（　　）
A．B．C．D．
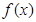定义在R上的函数，如果存在函数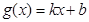(k,b为常数），使得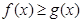对一切实数x都成立，则称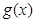为函数的一个承托函数．现有如下命题：
①对给定的函数，其承托函数可能不存在，也可能有无数个．
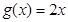②函数为函数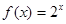的一个承托函数．
③定义域和值域都是R的函数不存在承托函数．
其中正确命题的序号是：(   )
A．①B．②C．①③D．②③
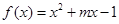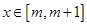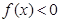已知函数，若对于任意的都有，则实数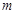的取值范围为      .
若一元二次不等式对一切实数都成立，则的取值范围为（  ）
A．B．C．D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网