题目内容
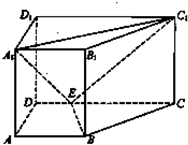
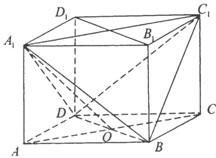
如图所示,在正方体ABCD-A1B1C1D1中,E是棱DD1的中点.
(1)求直线BE和直线CD所成角的余弦值;
(2)在棱C1D1上是否存在一点F,使B1F∥平面A1BE?证明你的结论.
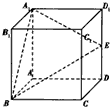
(1)求直线BE和直线CD所成角的余弦值;
(2)在棱C1D1上是否存在一点F,使B1F∥平面A1BE?证明你的结论.

(1)在正方体ABCD-A1B1C1D1中,由于AB∥CD,
故∠ABE(或其补角)即为直线BE和直线CD所成角.
设正方体的棱长为1,则由E是棱DD1的中点,可得AB=1,BE=
=
,
在Rt△ABE中,由余弦定理求得cos∠ABE=
=
.
(II)设AB1∩A1B=O,取C1D1中点F,连接OE、EB、B1F.根据三角形中位线定理,得EF∥C1D且EF=
C1D,平行四边形AB1C1D中,有B1O∥C1D且B1O=
C1D,
∴EF∥B1O且EF=B1O,四边形B1OEF为平行四边形,B1F∥OE,又B1F?平面A1BE,OE?平面A1BE,
∴B1F∥平面A1BE,
即存在C1D1中点F,使B1F∥平面A1BE.

故∠ABE(或其补角)即为直线BE和直线CD所成角.
设正方体的棱长为1,则由E是棱DD1的中点,可得AB=1,BE=
| BD2+DE2 |
| 3 |
| 2 |
在Rt△ABE中,由余弦定理求得cos∠ABE=
| AB |
| AE |
| 2 |
| 3 |
(II)设AB1∩A1B=O,取C1D1中点F,连接OE、EB、B1F.根据三角形中位线定理,得EF∥C1D且EF=
| 1 |
| 2 |
| 1 |
| 2 |
∴EF∥B1O且EF=B1O,四边形B1OEF为平行四边形,B1F∥OE,又B1F?平面A1BE,OE?平面A1BE,
∴B1F∥平面A1BE,
即存在C1D1中点F,使B1F∥平面A1BE.


练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目