题目内容
【题目】△ABC中,A、B、C的对边分别为a,b,c,面积为S,满足S= ![]() (a2+b2﹣c2).
(a2+b2﹣c2).
(1)求C的值;
(2)若a+b=4,求周长的范围与面积S的最大值.
【答案】
(1)解:∵S= ![]() absinC,cosC=
absinC,cosC= ![]() ,
,
即a2+b2﹣c2=2abcosC,
∴S= ![]() (a2+b2﹣c2)变形得:
(a2+b2﹣c2)变形得: ![]() absinC=
absinC= ![]() ×2abcosC,
×2abcosC,
整理得:tanC= ![]() ,
,
又0<C<π,
则C= ![]() ;
;
(2)解:a2+b2﹣c2=2abcosC,可得c2=(a+b)2﹣3ab=16﹣3ab,
由a+b=4≥2 ![]() (当且仅当a=b取等号),
(当且仅当a=b取等号),
即有0<ab≤4,
则c∈[2,4),
则周长的范围是[6,8);
△ABC的面积为S= ![]() absinC=
absinC= ![]() ab≤
ab≤ ![]() ,
,
当且仅当a=b=2,取得最大值 ![]() .
.
【解析】(1)运用三角形的面积公式和余弦定理,结合同角的商数关系,特殊角的三角函数值,可得角C;(2)运用余弦定理和基本不等式,以及三角形的面积公式,可得最大值.

 英才点津系列答案
英才点津系列答案 红果子三级测试卷系列答案
红果子三级测试卷系列答案【题目】上世纪八十年代初, 邓小平同志曾指出“在人才的问题上,要特别强调一下,必须打破常规去发现、选拔和培养杰出的人才”. 据此,经省教育厅批准,某中学领导审时度势,果断作出于1985年开始施行超常实验班教学试验的决定.一时间,学生兴奋,教师欣喜,家长欢呼,社会热议.该中学实验班一路走来,可谓风光无限,硕果累累,尤其值得一提的是,1990年,全国共招收150名少年大学生,该中学就有19名实验班学生被录取,占全国的十分之一,轰动海内外.设该中学超常实验班学生第x年被录取少年大学生的人数为y.
左下表为该中学连续5年实验班学生被录取少年大学生人数,求y关于x的线性回归方程,并估计第6年该中学超常实验班学生被录取少年大学生人数;
年份序号x | 1 | 2 | 3 | 4 | 5 |
录取人数y | 10 | 11 | 14 | 16 | 19 |
附1: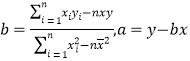
![]()
下表是从该校已经毕业的100名高中生录取少年大学生人数与是否接受超常实验班教育得到
2×2列联表,完成上表,并回答:是否有95%以上的把握认为“录取少年大学生人数与是否接受超常实验班教育有关系”.
附2:
接受超常实验班教育 | 未接受超常实验班教育 | 合计 | |
录取少年大学生 | 60 | 80 | |
未录取少年大学生 | 10 | ||
合计 | 30 | 100 |
![]()
| 0.50 | 0.40 | 0.10 | 005 |
| 0.455 | 0.708 | 2.706 | 3.841 |