ƒøƒ⁄»ð
°æƒø°ø…œ ¿ºÕ∞À ƃͥ˙≥ı£¨ µÀ–°∆ΩÕ¨÷摯÷∏≥ˆ°∞‘⁄»À≤≈µƒŒ Â…œ£¨“™Ãÿ±«øµ˜“ªœ¬£¨±ÿ–Î¥Ú∆∆≥£πÊ»•∑¢œ÷°¢—°∞Œ∫Õ≈ý—¯ΩÐ≥ˆµƒ»À≤≈°±. æð¥À£¨æ≠ °ΩÔ˝Ã¸≈˙◊º£¨ƒ≥÷–—ߡϵº…Û ±∂» ∆£¨π˚∂œ◊˜≥ˆ”⁄1985ƒÍø™ º ©––≥¨≥£ µ—È∞ýΩÃ—ß ‘—ȵƒæˆ∂®.“ª ±º‰£¨—ß…˙–À∑У¨Ωà ¶–¿œ≤£¨º“≥§ª∂∫Ù£¨…Áª·»»“È.∏√÷–—ß µ—È∞ý“ª¬∑◊þ¿¥£¨ø…ŒΩ∑Áπ‚ŒÞœÞ£¨À∂π˚¿€¿€£¨”»∆‰÷µµ√“ªÃ·µƒ «£¨1990ƒÍ£¨»´π˙π≤’– ’150√˚…ŸƒÍ¥Û—ß…˙£¨∏√÷–—ßæÕ”–19√˚ µ—È∞ý—ß…˙±ª¬º»°£¨’º»´π˙µƒ Æ∑÷÷Æ“ª£¨∫‰∂Ø∫£ƒ⁄Õ‚.…Ë∏√÷–—ß≥¨≥£ µ—È∞ý—ß…˙µ⁄xƒÍ±ª¬º»°…ŸƒÍ¥Û—ß…˙µƒ»À ˝Œ™y.
◊Ûœ¬±ÌŒ™∏√÷–—ß¡¨–¯5ƒÍ µ—È∞ý—ß…˙±ª¬º»°…ŸƒÍ¥Û—ß…˙»À ˝£¨«Ûyπÿ”⁄xµƒœþ–‘ªÿπÈ∑Ω≥ã¨≤¢π¿º∆µ⁄6ƒÍ∏√÷–—ß≥¨≥£ µ—È∞ý—ß…˙±ª¬º»°…ŸƒÍ¥Û—ß…˙»À ˝;
ƒÍ∑ð–Ú∫≈x | 1 | 2 | 3 | 4 | 5 |
¬º»°»À ˝y | 10 | 11 | 14 | 16 | 19 |
∏Ω1£∫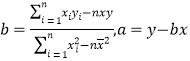
![]()
œ¬±Ì «¥”∏√–£“—æ≠±œ“µµƒ100√˚∏þ÷–…˙¬º»°…ŸƒÍ¥Û—ß…˙»À ˝”Î «∑ÒΩ” Ð≥¨≥£ µ—È∞ýΩÔ˝µ√µΩ
2°¡2¡–¡™±Ì£¨ÕÍ≥……œ±Ì£¨≤¢ªÿ¥£∫ «∑Ò”–95%“‘…œµƒ∞—Œ’»œŒ™°∞¬º»°…ŸƒÍ¥Û—ß…˙»À ˝”Î «∑ÒΩ” Ð≥¨≥£ µ—È∞ýΩÔ˝”–πÿœµ°±£Æ
∏Ω2£∫
Ω” Ð≥¨≥£ µ—È∞ýΩÔ˝ | Œ¥Ω” Ð≥¨≥£ µ—È∞ýΩÔ˝ | ∫œº∆ | |
¬º»°…ŸƒÍ¥Û—ß…˙ | 60 | 80 | |
Œ¥¬º»°…ŸƒÍ¥Û—ß…˙ | 10 | ||
∫œº∆ | 30 | 100 |
![]()
| 0.50 | 0.40 | 0.10 | 005 |
| 0.455 | 0.708 | 2.706 | 3.841 |
°æ¥∞∏°ø£®1£©21£®2£©”–95%µƒ∞—Œ’
°æΩ‚Œˆ°ø ‘Â∑÷Œˆ£∫£®1£©Ω´ ˝æð¥˙»ÎªÿπÈ÷±œþ∑Ω≥õƒº∆À„π´ Ω£¨œ»«Û≥ˆ![]() £¨‘Ÿ«Û≥ˆ
£¨‘Ÿ«Û≥ˆ![]() £¨”…¥Àµ√µΩªÿπÈ÷±œþ∑Ω≥ã¨Ω´
£¨”…¥Àµ√µΩªÿπÈ÷±œþ∑Ω≥ã¨Ω´![]() ¥˙»ÎªÿπÈ÷±œþ∑Ω≥㨺¥ø…«Ûµ√‘§≤‚÷µ.£®2£©Ω´
¥˙»ÎªÿπÈ÷±œþ∑Ω≥㨺¥ø…«Ûµ√‘§≤‚÷µ.£®2£©Ω´![]() ¡™±ÌÃÓ–¥π˛£¨¥˙»Î
¡™±ÌÃÓ–¥π˛£¨¥˙»Î![]() µƒº∆À„π´ Ω£¨º∆À„µ√
µƒº∆À„π´ Ω£¨º∆À„µ√![]() £¨π Œ“√«”–95%µƒ∞—Œ’»œŒ™°∞¬º»°…ŸƒÍ¥Û—ß…˙»À ˝”Î «∑ÒΩ” Ð≥¨≥£ µ—È∞ýΩÔ˝”–πÿœµ°±£Æ
£¨π Œ“√«”–95%µƒ∞—Œ’»œŒ™°∞¬º»°…ŸƒÍ¥Û—ß…˙»À ˝”Î «∑ÒΩ” Ð≥¨≥£ µ—È∞ýΩÔ˝”–πÿœµ°±£Æ
‘Ã‚Ω‚Œˆ£∫
£®1£©”…“—÷™÷– ˝æðø…µ√£∫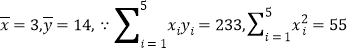
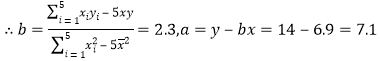
![]() µ±
µ±![]() ±
±![]()
º¥µ⁄6ƒÍ∏√–£ µ—È∞ý—ß…˙¬º»°…ŸƒÍ¥Û—ß…˙»À ˝‘ºŒ™21»À£ª
£®2£©∏√–£“—æ≠±œ“µµƒ100√˚∏þ÷–…˙¬º»°…ŸƒÍ¥Û—ß…˙»À ˝”Î «∑ÒΩ” Ð≥¨≥£ µ—È∞ýΩÔ˝µ√µΩ2°¡2¡–¡™±Ì£∫
Ω” Ð≥¨≥£ µ—È∞ýΩÔ˝ | Œ¥Ω” Ð≥¨≥£ µ—È∞ýΩÔ˝ | ∫œº∆ | |
¬º»°…ŸƒÍ¥Û—ß…˙ | 60 | 20 | 80 |
Œ¥¬º»°…ŸƒÍ¥Û—ß…˙ | 10 | 10 | 20 |
∫œº∆ | 70 | 30 | 100 |
∏˘æð¡–¡™±Ì÷–µƒ ˝æ𣨵√µΩ![]() µƒπ€≤‚÷µŒ™
µƒπ€≤‚÷µŒ™
![]()
π Œ“√«”–95%µƒ∞—Œ’»œŒ™°∞¬º»°…ŸƒÍ¥Û—ß…˙»À ˝”Î «∑ÒΩ” Ð≥¨≥£ µ—È∞ýΩÔ˝”–πÿœµ°±£Æ