题目内容
【题目】已知等差数列{an}的前n项和为Sn=n2+pn+q（p，q∈R），且a2 ， a3 ， a5成等比数列．
（1）求p，q的值；
（2）若数列{bn}满足an+log2n=log2bn ， 求数列{bn}的前n项和Tn ．
【答案】
（1）
解法一：
当n=1时，a1=S1=1+p+q，
当n≥2时，an=Sn﹣Sn﹣1…（2分）
=n2+pn+q﹣[（n﹣1）2+p（n﹣1）+q]
=2n﹣1+p．
∵{an}是等差数列，
∴1+p+q=2×1﹣1+p，得q=0．
又a2=3+p，a3=5+p，a5=9+p
∵a2，a3，a5成等比数列，
∴ 
，即（5+p）2=（3+p）（9+p），
解得p=﹣1．
解法二：
设等差数列{an}的公差为d，
则 
．
∵ 
，
∴ 
， 
，q=0．
∴d=2，p=a1﹣1，q=0．
∵a2，a3，a5成等比数列，
∴ ，
即 
．
解得a1=0．
∴p=﹣1．
（2）
解法一：
由（1）得an=2n﹣2．
∵an+log2n=log2bn，
∴ 
．
∴Tn=b1+b2+b3+…+bn﹣1+bn
=40+2×41+3×42+…+（n﹣1）4n﹣2+n4n﹣1，①
，②
①﹣②得 
= 
= 
．
∴ 
解法二：
由（1）得an=2n﹣2．
∵an+log2n=log2bn，
∴ ．
∴Tn=b1+b2+b3+…+bn﹣1+bn
=40+2×41+3×42+…+（n﹣1）4n﹣2+n4n﹣1．
由 
，
两边对x取导数得，
x0+2x1+3x2+…+nxn﹣1= 
．
令x=4，得 
．
∴ 
【解析】解法一：（1）a1=S1=1+p+q，an=Sn﹣Sn﹣1=2n﹣1+p，由此求出q=0，由a2 ， a3 ， a5成等比数列，得p=﹣1．（2）an=2n﹣2， ，由此利用错位相减法能求出数列{bn}的前n项和Tn ．
解法二：（1）由 ，得d=2，p=a1﹣1，q=0．由a2 ， a3 ， a5成等比数列，得p=﹣1．（2）an=2n﹣2. ，由 ，两边对x取导数得，由此能求出 ．
【考点精析】掌握数列的前n项和和等差数列的性质是解答本题的根本，需要知道数列{an}的前n项和sn与通项an的关系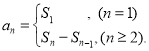
；在等差数列{an}中，从第2项起，每一项是它相邻二项的等差中项；相隔等距离的项组成的数列是等差数列．
