题目内容
16.△ABC中,a=$\sqrt{7}$,b=3,c=2,则∠A=( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
分析 由余弦定理cosA=$\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}$,代入数据,再由特殊角的三角函数值,计算即可得到A.
解答 解:由余弦定理直接得$cosA=\frac{{{b^2}+{c^2}-{a^2}}}{2bc}=\frac{9+4-7}{2×3×2}=\frac{1}{2}$,
且A∈(0°,180°),得A=60°,
故选C.
点评 本题考查余弦定理的运用,考查运算能力,属于基础题.

练习册系列答案
 计算高手系列答案
计算高手系列答案
相关题目
7.如图是计算1+2+4+…+219的值的一个程序框图,则其中空白判断框内应填入的是( )
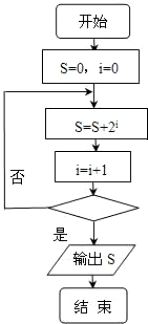

| A. | i=19 | B. | i≥20 | C. | i≤19 | D. | i≤20 |
4.在研究高血压与患心脏病的关系调查中,调查了有高血压者30人,其中有20人患心脏病;调查的80个不高血压者中有30人患心脏病,
(1)根据以上数据建立一个2×2的列联表;
(2)若认为“高血压与患心脏病有关”,则出错的概率会是多少?
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$;n=a+b+c+d
(1)根据以上数据建立一个2×2的列联表;
(2)若认为“高血压与患心脏病有关”,则出错的概率会是多少?
参考公式:K2=$\frac{n(ad-bc)^{2}}{(a+b)(c+d)(a+c)(b+d)}$;n=a+b+c+d
| P(K2>k) | 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k | 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.84 | 5.024 | 6.635 | 7.879 | 10.83 |
11.函数 f(x)=(x-2014)(x+2015)的图象与x轴,y轴有三个交点,有一个圆恰经过这三个点,则此圆与坐标轴的另一个交点是( )
| A. | (0,-1) | B. | (0,1) | C. | (0,$\sqrt{2014×2015}$) | D. | (0,$\sqrt{\frac{2014}{2015}}$) |
8.运行如图程序,若输入的是-2,则输出的结果是( )


| A. | 4 | B. | 2 | C. | -4 | D. | -2 |
5.已知命题p,q,那么“p∧q为真命题”是“p∨q为真命题”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |