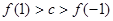题目内容
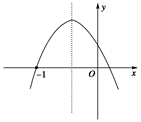
已知函数y=ax2+bx+c的图象如图所示,则的值为( )

| A.2b | B.a-b+c |
| C.-2b | D.0 |
C
试题分析:根据题意,由于函数y=ax2+bx+c的图象可知开口向下,所以a<0,同时再y轴上的截距为正数,故可知c>0,那么可知f(1)=a+b+c,f(0)=c,f(-1)=0=a-b+c,a+c=b,可知二次函数对应的方程有两个根,那么结合条件,那么可知对称轴小于零,可知b<0,因此的值-2b ,故选C.
点评:理解图像于性质之间的对应关系,主要是把握好对称轴的符号关系,以及开口即可,属于基础题。

练习册系列答案
相关题目
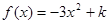 ,当实数
,当实数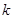 属于下列选项中的哪一个区间时,才能确保一定存在实数对
属于下列选项中的哪一个区间时,才能确保一定存在实数对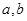 (
(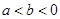 ),使得当函数
),使得当函数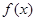 的定义域为
的定义域为 时,其值域也恰好是
时,其值域也恰好是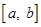 ( )
( )



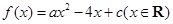 的值域为
的值域为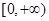 ,则
,则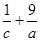 的最小值为
的最小值为



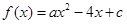 的值域为
的值域为 ,则
,则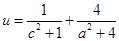 的最小值为 .
的最小值为 . 的结果是 .
的结果是 .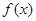 的最小值为1,且
的最小值为1,且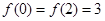 .
.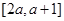 上不单调,求实数
上不单调,求实数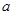 的取值范围;
的取值范围;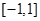 上,
上,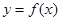 的图像恒在
的图像恒在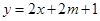 的图像上方,试确定实数
的图像上方,试确定实数 的取值范围.
的取值范围. ,求实数m的取值范围.
,求实数m的取值范围. ,且
,且 .则( )
.则( )