题目内容
设满足条件x2+y2≤1的点(x,y)构成的平面区域的面积为S1,满足条件[x]2+[y]2≤1的点(x,y)构成的平面区域的面积为S2(其中[x],[y]分别表示不大于x,y的最大整数,例如[-0.3]=-1,[1.2]=1),给出下列结论:
①点(S1,S2)在直线y=x左上方的区域内;
②点(S1,S2)在直线x+y=7左下方的区域内;
③S1<S2;
④S1>S2.
其中所有正确结论的序号是______.
①点(S1,S2)在直线y=x左上方的区域内;
②点(S1,S2)在直线x+y=7左下方的区域内;
③S1<S2;
④S1>S2.
其中所有正确结论的序号是______.
满足条件x2+y2≤1的点(x,y)构成的平面区域为一个圆,其面积为:π
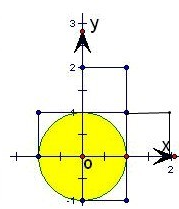
当0≤x<1,0≤y<1时,满足条件[x]2+[y]2≤1;
当0≤x<1,1≤y<2时,满足条件[x]2+[y]2≤1;
当0≤x<1,-1≤y<0时,满足条件[x]2+[y]2≤1;
当-1≤x<0,0≤y<1时,满足条件[x]2+[y]2≤1;
当0≤y<1,1≤x<2时,满足条件[x]2+[y]2≤1;
∴满足条件[x]2+[y]2≤1的点(x,y)构成的平面区域是五个边长为1的正方形,其面积为:5
综上得:S1与S2的关系是S1<S2,点(S1,S2)一定在直线y=x左上方的区域内
故答案为:①③.
当0≤x<1,0≤y<1时,满足条件[x]2+[y]2≤1;
当0≤x<1,1≤y<2时,满足条件[x]2+[y]2≤1;
当0≤x<1,-1≤y<0时,满足条件[x]2+[y]2≤1;
当-1≤x<0,0≤y<1时,满足条件[x]2+[y]2≤1;
当0≤y<1,1≤x<2时,满足条件[x]2+[y]2≤1;
∴满足条件[x]2+[y]2≤1的点(x,y)构成的平面区域是五个边长为1的正方形,其面积为:5
综上得:S1与S2的关系是S1<S2,点(S1,S2)一定在直线y=x左上方的区域内
故答案为:①③.


练习册系列答案
相关题目
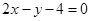 上,若圆M上不存在点N,使
上,若圆M上不存在点N,使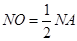 ,其中A(0,3),则圆心M横坐标的取值范围 .
,其中A(0,3),则圆心M横坐标的取值范围 .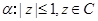 ,
, .若
.若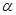 是
是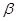 的充分非必要条件,则实数
的充分非必要条件,则实数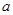 的取值范围是( )
的取值范围是( )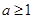
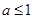
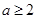
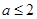
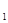 :
: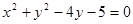 与圆
与圆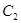 :
: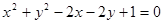 位置关系是( )
位置关系是( )