题目内容
已知定点A(-2,-4),过点A作倾斜角为45 的直线l,交抛物线y2=2px(p>0)于B、C两点,且|BC|=210.(Ⅰ)求抛物线的方程;(Ⅱ)在(Ⅰ)中的抛物线上是否存在点D,使得|DB|=|DC|成立?如果存在,求出点D的坐标;如果不存在,请说明理由.
(Ⅰ) y2=2x. (Ⅱ) 见解析
(Ⅰ)直线l方程为y=x-2,将其代入y2=2px,并整理,得
x2-2(2+p)x+4=0…①,∵p>0,∴△=4(2+p)2-16>0,
设B(x1,y1)、C(x2,y2),∴x1+x2=4+2p,x1·x2=4,∵|BC|=210,而|BC|=1+k2|x1-x2|,
∴22p2+4p=210,解得p=1,∴抛物线方程y2=2x.
(Ⅱ)假设在抛物线y2=2x上存在点D(x3,y3),使得|DB|=|DC|成立,
记线段BC中点为E(x0,y0),则|DB|=|DC| DE⊥BC kDE=-1k1=-1,
当p=1时,①式成为x2-6x+4=0,∴x0=x1+x22=3,y0=x0-2=1,
∴点D(x3,y3)应满足 y23=2x3y3-1x3-3=-1,解得 x3=2y3=2或 x3=8y3=-4.
∴存在点D(2,2)或(8,-4),使得|DB|=|DC|成立.
(Ⅰ)直线l方程为y=x-2,将其代入y2=2px,并整理,得
x2-2(2+p)x+4=0…①,∵p>0,∴△=4(2+p)2-16>0,
设B(x1,y1)、C(x2,y2),∴x1+x2=4+2p,x1·x2=4,∵|BC|=210,而|BC|=1+k2|x1-x2|,
∴22p2+4p=210,解得p=1,∴抛物线方程y2=2x.
(Ⅱ)假设在抛物线y2=2x上存在点D(x3,y3),使得|DB|=|DC|成立,
记线段BC中点为E(x0,y0),则|DB|=|DC| DE⊥BC kDE=-1k1=-1,
当p=1时,①式成为x2-6x+4=0,∴x0=x1+x22=3,y0=x0-2=1,
∴点D(x3,y3)应满足 y23=2x3y3-1x3-3=-1,解得 x3=2y3=2或 x3=8y3=-4.
∴存在点D(2,2)或(8,-4),使得|DB|=|DC|成立.

练习册系列答案
相关题目
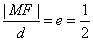
 ,设动点M的轨迹为曲线C.
,设动点M的轨迹为曲线C. 与曲线C交于P,Q两点,若
与曲线C交于P,Q两点,若 ,证明:
,证明: 为定值.
为定值.