题目内容
(本小题满分12分)在平面直角坐标系xOy中,已知定点A(-2,0)、B(2,0),M是动点,且直线MA与直线MB的斜率之积为 ,设动点M的轨迹为曲线C.
,设动点M的轨迹为曲线C.
(I)求曲线C的方程;
(II)过定点T(-1,0)的动直线 与曲线C交于P,Q两点,若
与曲线C交于P,Q两点,若 ,证明:
,证明: 为定值.
为定值.
【答案】
(Ⅰ)设动点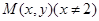 ,则
,则 ,……………2分
,……………2分
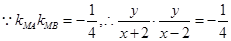 ,
,
即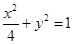 (
(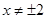 ).…………………4分
).…………………4分
(Ⅱ)当 的斜率不存在时,
的斜率不存在时,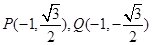 ,
,
若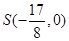 ,
,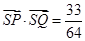 .………………6分
.………………6分
当直线 的斜率存在时,设
的斜率存在时,设 的方程为
的方程为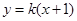 ,
,  ,联立方程组
,联立方程组
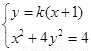 ,消去
,消去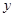 得
得 ,
,
设 ,则
,则 ………………8分
………………8分
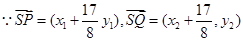 .
.
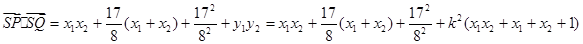
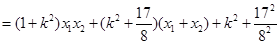 ,
,
 ……………10分
……………10分

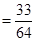 .…………………12分
.…………………12分
【解析】(I)根据动点满足的几何条件进行坐标化建立方程,然后化简即可得到曲线C的方程。但化简方程时要注意等价转化。
(II)直线方程与曲线C的方程联立消元后,根据韦达定理对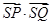 进行坐标化,即可证明。
进行坐标化,即可证明。

练习册系列答案
 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案 暑假作业安徽少年儿童出版社系列答案
暑假作业安徽少年儿童出版社系列答案
相关题目