题目内容
已知定点A(-2,
),F是椭圆
+
=1的右焦点,在椭圆上求一点M,使|AM|+2|MF|取得最小值.
| 3 |
| x2 |
| 16 |
| y2 |
| 12 |
分析:利用椭圆的第二定义则
=e=
将|AM|+2|MF|转化为|AM|+|MN|,当A,M,N同时在垂直于右准线的一条直线上时,|AM|+2|MF|取得最小值.
| |MF| |
| |MN| |
| 1 |
| 2 |
解答:解:显然椭圆
+
=1的a=4,c=2,e=
,记点M到右准线的距离为|MN|,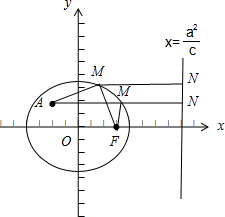
则
=e=
,|MN|=2|MF|,即|AM|+2|MF|=|AM|+|MN|,
当A,M,N同时在垂直于右准线的一条直线上时,|AM|+2|MF|取得最小值,
此时My=Ay=
,代入到
+
=1得Mx=±2
,
而点M在第一象限,
∴M(2
,
).
| x2 |
| 16 |
| y2 |
| 12 |
| 1 |
| 2 |

则
| |MF| |
| |MN| |
| 1 |
| 2 |
当A,M,N同时在垂直于右准线的一条直线上时,|AM|+2|MF|取得最小值,
此时My=Ay=
| 3 |
| x2 |
| 16 |
| y2 |
| 12 |
| 3 |
而点M在第一象限,
∴M(2
| 3 |
| 3 |
点评:本题考查椭圆的简单性质,考查椭圆第二定义的应用,考查等价转化的思想,考查作图能力,属于中档题.

练习册系列答案
相关题目
 已知定点A
已知定点A