题目内容

已知定点A(2,0),点Q是圆x2+y2=1上的动点,∠AOQ的平分线交AQ于M,当点Q在圆上移动时,求动点M的轨迹方程.

解析:由三角形内角平分线的性质知=2,则M分所成的比为λ=,设Q(x1,y1),M(x,y).

则有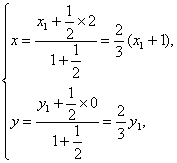即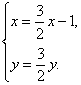

又Q(x1,y1)在圆x2+y2=1上,则有x12+y12=1.

将上式代入得(x-1)2+(y)2=1,故动点M的轨迹方程为(x-)2+y2=()2(y≠0).

练习册系列答案
相关题目
已知定点A（0，1）、B（0，-1）、C（1，0），动点P满足：
AP
•
BP
=k|
PC
|2（k∈R）．
（1）求动点P的轨迹方程，并说明方程表示的图形；
（2）当k=2时，求|
AP
+
BP
|的最大值和最小值．
（2009•大连二模）已知定点A（0，2），B（0，-2），C（2，0），动点P满足：
AP
•
BP
=m|
pc
|2
（I）求动点P的轨迹方程，并说明方程表示的曲线类型；
（II）当m=2时，设点P（x，y）（y≥0），求
y
x-8
的取值范围．
在平面直角坐标系XOY中，已知定点A（0，a），B（0，-a），M，N是x轴上两个不同的动点，
OM
•
ON
=4a2(a∈R，a≠0)，直线AM与直线BN交于C点．
（1）求点C的轨迹方程；
（2）若存在过点（0，-1）且不与坐标轴垂直的直线l与点C的轨迹交于不同的两点E、F，且|AE|=|AF|，求实数a的取值范围．

已知定点A(2,0)，圆O的方程为x2＋y2＝8，动点m在圆O上，那么∠OMA的最大值是

[　　]

A．

B．

C．

D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网