题目内容
已知定点A(-2，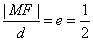
)，点F为椭圆
=1的右焦点，点M的椭圆上移动时，求|AM|+2|MF|的最小值，并求此时点M的坐标.
解析：由椭圆方程，得a=4,b=2,c=2,
∴e=,右焦点F(2，0)，右准线l：x=8.
设点M到右准线l的距离为d,则,即|2MF|=d.
∴|AM|+2|MF|=|AM|+d.
由于A在椭圆内，过A作AK⊥l，K为垂足，易证|AM|即为|AM|+d的最小值，其值为8-(-2)=10.
此时M点纵坐标为
，得横坐标为2
.
∴|AM|+2|MF|的最小值为10，这时点M的坐标为(2
，
).
温馨提示
(1)转化是一种重要的数学思想，本题利用第二定义，将看似没有“出路”的问题巧妙地化解了.
(2)本题实际上要求对椭圆的第二定义有深刻的理解，在后面的双曲线、抛物线中也有类似问题，注意总结规律.
练习册系列答案
科学实验活动册系列答案
相关题目
，设动点M的轨迹为曲线C.
与曲线C交于P,Q两点，若
，证明：
为定值.