题目内容
如图所示,圆柱的高为2,底面半径为 ,AE、DF是圆柱的两条母线,过
,AE、DF是圆柱的两条母线,过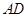 作圆柱的截面交下底面于
作圆柱的截面交下底面于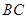 ,四边形ABCD是正方形.
,四边形ABCD是正方形.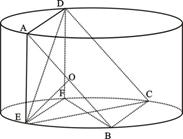
(Ⅰ)求证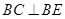 ;
;
(Ⅱ)求四棱锥E-ABCD的体积.
(Ⅰ)详见解析;(Ⅱ)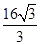
解析试题分析:(Ⅰ)根据AE是圆柱的母线,所以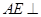 下底面,又
下底面,又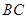
 下底面,则
下底面,则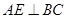
又截面ABCD是正方形,所以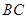 ⊥
⊥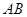 ,又
,又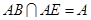

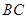 ⊥面
⊥面 ,又
,又 面
面 ,即可得到BC⊥BE;
,即可得到BC⊥BE;
(Ⅱ)根据锥体的体积公式即可求四棱锥E-ABCD的体积.
试题解析:(Ⅰ) AE是圆柱的母线,
AE是圆柱的母线,
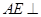 下底面,又
下底面,又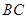
 下底面,
下底面,
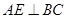 .3分
.3分
又 截面ABCD是正方形,所以
截面ABCD是正方形,所以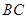 ⊥
⊥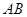 ,又
,又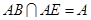

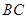 ⊥面
⊥面 ,又
,又 面
面 ,
,
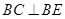 (7分)
(7分)
(Ⅱ)因为母线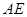 垂直于底面,所以
垂直于底面,所以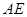 是三棱锥
是三棱锥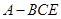 的高 (8分),
的高 (8分),
由(Ⅰ)知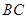 ⊥面
⊥面 ,
, 面
面 ,
, 面
面 ⊥面
⊥面 ,
,
又 面
面
 面
面
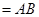 ,
, 面
面 ,
,

 面
面 ,即EO就是四棱锥
,即EO就是四棱锥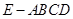 的高 (10分)
的高 (10分)
设正方形 的边长为
的边长为 , 则
, 则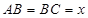 ,
,
又
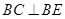 ,
,

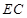 为直径,即
为直径,即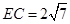
在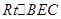 中,
中,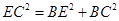 , 即
, 即

 , (12分)
, (12分)

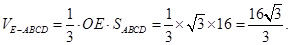
考点:1.棱柱、棱锥、棱台的体积;2.空间中直线与直线之间的垂直关系.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
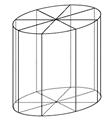

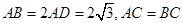 ,F是AB上的一点,且
,F是AB上的一点,且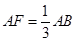 ,将圆沿AB折起,使点C在平面ABD的射影E在BD上,已知
,将圆沿AB折起,使点C在平面ABD的射影E在BD上,已知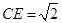
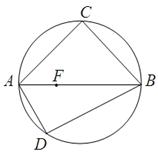
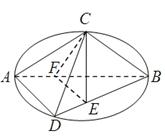
 平面BCE
平面BCE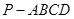 中,底面
中,底面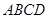 是菱形,
是菱形,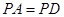 ,
,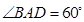 ,
,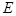 是
是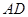 的中点,点
的中点,点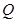 在侧棱
在侧棱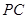 上.
上.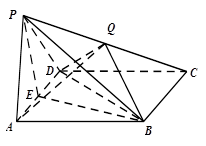
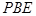 ;
; //平面
//平面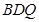 ;
;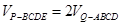 ,试求
,试求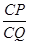 的值.
的值. =2,点G为AC的中点.
=2,点G为AC的中点.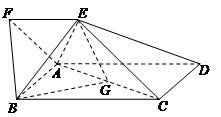
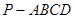 中,
中,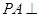 平面
平面 ,底面
,底面 是平行四边形,
是平行四边形,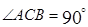 ,
,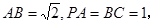
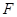 是
是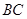 的中点
的中点
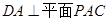
 上确定一点
上确定一点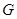 ,使
,使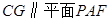 ,求三棱锥
,求三棱锥 的体积.
的体积.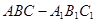 的三视图如图所示,且
的三视图如图所示,且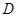 是
是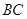 的中点.
的中点.
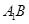 ∥平面
∥平面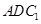 ;
;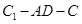 的余弦值;
的余弦值;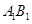 上是否存在点
上是否存在点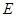 ,使
,使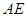 与
与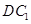 成
成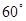 角?若存在,确定
角?若存在,确定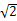 ,AA1=3,E为CD上一点,DE=1,EC=3
,AA1=3,E为CD上一点,DE=1,EC=3
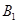 到平面EA1C1的距离.
到平面EA1C1的距离.