题目内容
8.在△ABC中,角A、B、C的对边分别为a、b、c,若a2-c2=2b且tanA=3tanC,则b=4.分析 已知第二个等式利用同角三角函数间的基本关系化简,再利用正弦、余弦定理化简,整理得到关系式,把第一个等式代入求出b的值即可.
解答 解:∵tanA=3tanC,
∴$\frac{sinA}{cosA}$=$\frac{3sinC}{cosC}$,即$\frac{sinA}{3sinC}$=$\frac{cosA}{cosC}$,
∴$\frac{a}{3c}$=$\frac{\frac{{b}^{2}+{c}^{2}-{a}^{2}}{2bc}}{\frac{{a}^{2}+{b}^{2}-{c}^{2}}{2ab}}$,
整理得:b2=2(a2-c2),
∵a2-c2=2b,
∴b2=4b,
解得:b=4或b=0(舍去),
则b=4.
故答案为:4
点评 此题考查了正弦、余弦定理,以及同角三角函数间的基本关系,熟练掌握正弦、余弦定理是解本题的关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案
相关题目
 如图,在四棱锥P-ABCD中,PC⊥底面ABCD.底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2,AD=CD=1,E是线段PB的中点.
如图,在四棱锥P-ABCD中,PC⊥底面ABCD.底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2,AD=CD=1,E是线段PB的中点.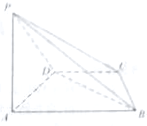 如图,在四棱锥P-ABCD中,底面ABCD为等腰梯形,且满足AB∥CD,AD=DC=$\frac{1}{2}$AB,PA⊥平面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD为等腰梯形,且满足AB∥CD,AD=DC=$\frac{1}{2}$AB,PA⊥平面ABCD. 某同学在社会实践中,为了测量一湖泊两侧A、B间的距离,某同学首先选定了与A、B不共线的一点C,然后给出了四种测量方案(△ABC的内角A、B、C所对的边分别记为 a、b、c):
某同学在社会实践中,为了测量一湖泊两侧A、B间的距离,某同学首先选定了与A、B不共线的一点C,然后给出了四种测量方案(△ABC的内角A、B、C所对的边分别记为 a、b、c):