题目内容
16. 如图,在四棱锥P-ABCD中,PC⊥底面ABCD.底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2,AD=CD=1,E是线段PB的中点.
如图,在四棱锥P-ABCD中,PC⊥底面ABCD.底面ABCD是直角梯形,AB⊥AD,AB∥CD,AB=2,AD=CD=1,E是线段PB的中点.(Ⅰ)证明:AC⊥平面PBC;
(Ⅱ)若点P到平面ACE的距离是$\frac{{\sqrt{6}}}{3}$,求三棱锥P-ACD的体积.
分析 (I)取AB的中点M,连接CM,由已知可得:四边形CDAM是正方形,CM=MA=MB,可得AC⊥CB,PC⊥底面ABCD,于是PC⊥AC,即可证明AC⊥平面PBC;
(II)在平面PBC内作PH⊥CE,垂足为H.由(I)可得:平面PBC⊥平面PBC,在平面PBC内作PH⊥CE,垂足为H,可得PH⊥平面ACE,PH=$\frac{\sqrt{6}}{3}$.设PC=t,S△PCE=$\frac{1}{2}{S}_{△PBC}$=$\frac{\sqrt{2}}{4}t$.又${S}_{△PCE}=\frac{1}{2}CE•PH$,解得t,即可VP-ACD=$\frac{1}{3}•{S}_{△ACD}$•PC.
解答 (I)证明:取AB的中点M,连接CM,
∵AM=$\frac{1}{2}$AB=1=CD=AD,AB⊥AD,AB∥CD,
∴四边形CDAM是正方形,CM=MA=MB,
∴AC⊥CB,
∵PC⊥底面ABCD,
∴PC⊥AC,又PC∩BC=C,
∴AC⊥平面PBC;
(II)解:在平面PBC内作PH⊥CE,垂足为H.
由(I)可得:平面PBC⊥平面AEC,
在平面PBC内作PH⊥CE,垂足为H,则PH⊥平面ACE,
∴PH=$\frac{\sqrt{6}}{3}$.设PC=t,则PB=$\sqrt{2+{t}^{2}}$,CE=$\frac{1}{2}PB$=$\frac{1}{2}\sqrt{2+{t}^{2}}$,
同时,S△PBC=$\frac{1}{2}•\sqrt{2}•t$,S△PCE=$\frac{1}{2}{S}_{△PBC}$=$\frac{\sqrt{2}}{4}t$.
又${S}_{△PCE}=\frac{1}{2}CE•PH$,
有$\frac{1}{2}•\frac{\sqrt{2+{t}^{2}}}{2}•\frac{\sqrt{6}}{3}=\frac{\sqrt{2}}{4}t$,解得t=1,即PC=1,
∴VP-ACD=$\frac{1}{3}•{S}_{△ACD}$•PC=$\frac{1}{6}$.
点评 本题考查了线面垂直的判定与性质定理、正方形的性质、直角三角形的性质、“等积变形”、三棱锥的体积计算公式,考查了推理能力与体积计算公式,属于中档题.

| A. | $\sqrt{2}$ | B. | -$\sqrt{2}$ | C. | 2 | D. | -2 |
| A. | $\frac{7}{9}$ | B. | ±3 | C. | 3 | D. | -3 |
 如图,在三棱锥P-ABC中,PA⊥平面ABC,BC⊥PB.
如图,在三棱锥P-ABC中,PA⊥平面ABC,BC⊥PB.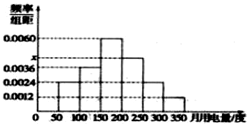 利用简单随机抽样从某小区抽取100户居民进行月用电量调查,发现其用电量都在50到350度之间,频率分布直方图如图所示.在这些用户中,用电量落在区间[150,250]内的户数为( )
利用简单随机抽样从某小区抽取100户居民进行月用电量调查,发现其用电量都在50到350度之间,频率分布直方图如图所示.在这些用户中,用电量落在区间[150,250]内的户数为( )