题目内容
12. 如图,在四棱锥P-ABCD中,底面ABCD为等腰梯形,且满足AB∥CD,AD=DC=$\frac{1}{2}$AB,PA⊥平面ABCD.
如图,在四棱锥P-ABCD中,底面ABCD为等腰梯形,且满足AB∥CD,AD=DC=$\frac{1}{2}$AB,PA⊥平面ABCD.(Ⅰ)求证:平面PBD⊥平面PAD;
(Ⅱ)若PA=AB,求直线PC与平面PAD所成角的正弦值.
分析 (Ⅰ)首先利用中点得到△BCE为正三角形,进一步利用勾股定理的逆定理得到线线垂直,再利用线面垂直的判定定理证得:线面垂直.最后转化成面面垂直.
(Ⅱ)首先作出直线与平面的夹角的平面角,进一步利用解直角三角形知识求得结果.
解答 (Ⅰ)证明:取AB的中点,连接CE,则由题意知:△BCE为正三角形,
所以:∠ABC=60°,
由等腰梯形知:∠BCD=120°,设AD=CD=BC=2,则:AB=4,BD=2$\sqrt{3}$,
故:AD2+BD2=AB2,即得:∠ADB=90°,
所以:AD⊥BD,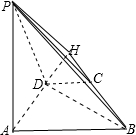
又因为:PA⊥平面ABCD,
所以:PA⊥BD,
则:BD⊥平面PAD,且BC?平面PBD,
所以:平面PBD⊥平面PAD.
(Ⅱ)在平面ABCD中,过点C作CH∥BD交AD的延长线于点H,
由(Ⅰ)知:BD⊥平面PAD,所以:CH⊥平面PAD,连接PH,
则:∠CPH即为所求的角.
在Rt△CHD中,CD=2,∠CDH=60°,
所以:CH=$\sqrt{3}$,
在Rt△PHC中,PC=$\sqrt{{PA}^{2}+{AC}^{2}}=2\sqrt{7}$,
所以:在Rt△PHC中,sin∠CPH=$\frac{CH}{PC}$=$\frac{\sqrt{3}}{2\sqrt{7}}=\frac{\sqrt{21}}{14}$.
即:直线PC与平面PAD所成角的正弦值为$\frac{\sqrt{21}}{14}$.
点评 本题考查的知识要点:勾股定理逆定理的应用,现面向垂直的判定和性质定理的应用,面面垂直的判定定理的应用,线面的夹角的应用.主要考查学生的空间想象能力和应用能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.有ab为两个运动,他们的合运动为c,则下列说法正确的是 ( )
| A. | 若a、b的轨迹为直线,则c的轨迹必为直线 | |
| B. | 若c的轨迹为直线,则a、b必为匀速运动 | |
| C. | 若a为匀速直线运动,b为匀速直线运动,则c必为匀速直线运动 | |
| D. | 若a、b均为初速度为零的匀变速直线运动,则c必为匀变速直线运动 |
4.双曲线C1:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)与抛物线C2:y2=2px(p>0)相交于A,B两点,公共弦AB恰过它们公共焦点F,则双曲线的一条渐近线的倾斜角所在的区间可能是( )
| A. | ($\frac{π}{3}$,$\frac{π}{2}$) | B. | ($\frac{π}{4}$,$\frac{π}{3}$) | C. | ($\frac{π}{6}$,$\frac{π}{4}$) | D. | (0,$\frac{π}{6}$) |
2.定义域为R的函数f(x)满足f(x+2)=2f(x)-2,当x∈(0,2]时,f(x)=$\left\{\begin{array}{l}{x^2}-x\;\;,\;\;x∈({0,1})\\ \frac{1}{x}\;,\;\;\;\;x∈[{1,2}]\end{array}$,若x∈(0,4]时,t2-$\frac{7t}{2}$≤f(x)≤3-t恒成立,则实数t的取值范围是( )
| A. | [2,+∞) | B. | $(1,\frac{5}{2})$ | C. | $(2,\frac{5}{2})$ | D. | [1,2] |
 如图,在三棱锥P-ABC中,PA⊥平面ABC,BC⊥PB.
如图,在三棱锥P-ABC中,PA⊥平面ABC,BC⊥PB. 已知斜四棱柱ABCD-A1B1C1D1的底面是矩形,侧面CC1D1D垂直底面ABCD,BC=2AB=DC1=2,BD1=2$\sqrt{3}$
已知斜四棱柱ABCD-A1B1C1D1的底面是矩形,侧面CC1D1D垂直底面ABCD,BC=2AB=DC1=2,BD1=2$\sqrt{3}$