题目内容
底面边长为1、侧棱长为2的正四棱柱ABCD-A1B1C1D1的8个顶点都在球O的表面上,E是侧棱AA1的中点,F是正方形ABCD的中心,则直线EF被球O所截得的线段长为
.
| ||
| 3 |
| ||
| 3 |
分析:由题意可知正方体的体对角线计算球的直径,求出对角线的长可得球的直径,求出半径.再利用勾股定理推导出EF=
,球心O到EF的距离为
,由此能求出结果.
| ||
| 2 |
| ||
| 3 |
解答:解:∵底面边长为1、侧棱长为2的正四棱柱ABCD-A1B1C1D1的8个顶点都在球O的表面上,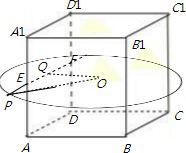
∴球O的半径R=
=
,
由已知所求EF是正方体在球中其中一个截面的直径,
∵OQ=
,EQ=
,∴OE=
=
,
∵AF=
AC=
,∴EF=
=
,
由球心O、E、F构成的△OEF中,
OF=
=1,
设球心O到EF的距离为d,则
×OE×OF=
×EF×d,
∴d=
=
.
所以直线EF被球O所截得的线段长=
×2=
.
故答案为:
.

∴球O的半径R=
| ||
| 2 |
| ||
| 2 |
由已知所求EF是正方体在球中其中一个截面的直径,
∵OQ=
| 1 |
| 2 |
| 1 |
| 2 |
|
| ||
| 2 |
∵AF=
| 1 |
| 2 |
| ||
| 2 |
1+
|
| ||
| 2 |
由球心O、E、F构成的△OEF中,
OF=
(
|
设球心O到EF的距离为d,则
| 1 |
| 2 |
| 1 |
| 2 |
∴d=
| ||||||
|
| ||
| 3 |
所以直线EF被球O所截得的线段长=
(
|
| ||
| 3 |
故答案为:
| ||
| 3 |
点评:本题考查正方体的外接球,球的表面积的计算,球的截面知识,考查计算能力,空间想象能力,正确利用条件求解直线EF被球O截得的线段长,是本题的难点,结合图形直观,易于解题.

练习册系列答案
相关题目
正六棱柱ABCDEF-A1B1C1D1E1F1的底面边长为1,侧棱长为
,则这个棱柱侧面对角线E1D与BC1所成的角是( )
| 2 |
| A、90° | B、60° |
| C、45° | D、30° |
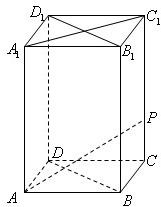 如图,在底面边长为1,侧棱长为2的正四棱柱ABCD-A1B1C1D1中,P是侧棱CC1上的一点,CP=m.
如图,在底面边长为1,侧棱长为2的正四棱柱ABCD-A1B1C1D1中,P是侧棱CC1上的一点,CP=m.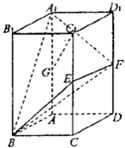 如图,正四棱柱ABCD-A1B1C1D1的底面边长为1,侧棱长为2,E、F、G分别CC1、DD1、AA1中点.
如图,正四棱柱ABCD-A1B1C1D1的底面边长为1,侧棱长为2,E、F、G分别CC1、DD1、AA1中点.