题目内容
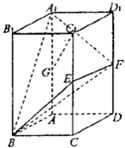 如图,正四棱柱ABCD-A1B1C1D1的底面边长为1,侧棱长为2,E、F、G分别CC1、DD1、AA1中点.
如图,正四棱柱ABCD-A1B1C1D1的底面边长为1,侧棱长为2,E、F、G分别CC1、DD1、AA1中点.①求证:A1F⊥面BEF;②求证:GC1∥面BEF;③求直线A1B与面BEF所成的角.
分析:①先根据条件得到EF⊥A1F;再结合边长之间的关系得到A1F⊥AF即可证:A1F⊥面BEF;
②先证四边形GAEC1为平行四边形即可得到GC1∥面BEF;
③结合第一问的结论求∠A1BF即可得到答案.
②先证四边形GAEC1为平行四边形即可得到GC1∥面BEF;
③结合第一问的结论求∠A1BF即可得到答案.
解答: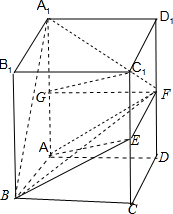 解:①∵正四棱柱ABCD-A1B1C1D1;
解:①∵正四棱柱ABCD-A1B1C1D1;
∴CD⊥平面ADD1A1;
又E、F、G分别CC1、DD1、AA1中点.
∴EF
CD
AB⇒E,F,A,B四点共面,且EF⊥平面ADD1A1,
所以EF⊥A1F (1);
而GF=
AA1,所以三角形AA1F为直角三角形且A1F⊥AF (2)
且AF∩EF=F⇒A1F⊥面AEF;
又由上得E,F,A,B四点共面
∴A1F⊥面BEF;
②∵GA=
AA1,C1E=
CC1;
∴GA
C1E,所以四边形GAEC1为平行四边形,⇒GC1∥AE
又因为GC1不在平面BEF内,又由上得E,F,A,B四点共面
而AE在平面BEF内;
∴GC1∥面BEF;
③∵A1F⊥面BEF
∴∠A1BF即为直线A1B与面BEF所成的角,
在直角三角形A1BF中
A1B=
=
,A1F=
=
,
∴sin∠A1BF=
=
=
⇒∠A1BF=arcsin
.
即直线A1B与面BEF所成的角为arcsin
.
 解:①∵正四棱柱ABCD-A1B1C1D1;
解:①∵正四棱柱ABCD-A1B1C1D1;∴CD⊥平面ADD1A1;
又E、F、G分别CC1、DD1、AA1中点.
∴EF
| ||
. |
| ||
. |
所以EF⊥A1F (1);
而GF=
| 1 |
| 2 |
且AF∩EF=F⇒A1F⊥面AEF;
又由上得E,F,A,B四点共面
∴A1F⊥面BEF;
②∵GA=
| 1 |
| 2 |
| 1 |
| 2 |
∴GA
| ||
. |
又因为GC1不在平面BEF内,又由上得E,F,A,B四点共面
而AE在平面BEF内;
∴GC1∥面BEF;
③∵A1F⊥面BEF
∴∠A1BF即为直线A1B与面BEF所成的角,
在直角三角形A1BF中
A1B=
| AB2+AA 12 |
| 5 |
| AG2+GF2 |
| 2 |
∴sin∠A1BF=
| A1F |
| A1B |
| ||
|
| ||
| 5 |
| ||
| 5 |
即直线A1B与面BEF所成的角为arcsin
| ||
| 5 |
点评:本题主要考察线面垂直,线面平行的证明以及直线与平面所成的角.解决线面平行的常用方法是转化为线线平行.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
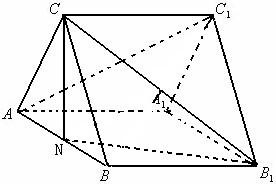 如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
 如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
如图是正三棱柱ABC-A1B1C1,AA1=3,AB=2,若N为棱AB中点.
