题目内容
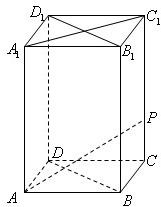 如图,在底面边长为1,侧棱长为2的正四棱柱ABCD-A1B1C1D1中,P是侧棱CC1上的一点,CP=m.
如图,在底面边长为1,侧棱长为2的正四棱柱ABCD-A1B1C1D1中,P是侧棱CC1上的一点,CP=m.(Ⅰ)试确定m,使直线AP与平面BDD1B1所成角为60°;
(Ⅱ)在线段A1C1上是否存在一个定点Q,使得对任意的m,D1Q⊥AP,并证明你的结论.
分析:(1)以D点为坐标原点,DA为x轴,DC为y轴,DD1为z轴建立空间坐标系,求出面BDD1B1的一个法向量
,以及
,求出这两向量的夹角,最后求出此角的补角即可;
(2)假设在A1C1上存在这样的点Q,设此点的横坐标为x,对任意的m要使D1Q在平面APD1上的射影垂直于AP.等价于
•
=0,建立等量关系,求出x即可.
| AC |
| AP |
(2)假设在A1C1上存在这样的点Q,设此点的横坐标为x,对任意的m要使D1Q在平面APD1上的射影垂直于AP.等价于
| AP |
| D1Q |
解答: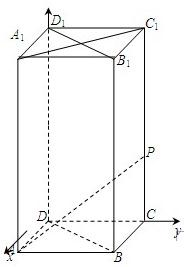 解:(1)建立如图所示的空间直角坐标系,则
解:(1)建立如图所示的空间直角坐标系,则
A(1,0,0),B(1,1,0),
P(0,1,m),C(0,1,0),
D(0,0,0),B1(1,1,2),D1(0,0,2).
所以
=(-1,-1,0),
=(0,0,2),
=(-1,1,m),
=(-1,1,0).
又由
•
=0,
•
=0知
为平面B
D的一个法向量.
设AP与面BDD1B1所成的角为θ,
则sinθ=cos(
-θ)=
=
=
,
解得m=
.故当m=
时,
直线AP与平面BDD1B1所成角为60°;(5分)
(2)若在A1C1上存在这样的点Q,设此点的横坐标为x,
则Q(x,1-x,2),
=(x,1-x,0).
依题意,对任意的m要使D1Q在平面APD1上的射影垂直于AP.等价于
⊥
?
•
=0?-x+(1-x)=0?x=
即Q为A1C1的中点时,满足题设的要求.(10分)
 解:(1)建立如图所示的空间直角坐标系,则
解:(1)建立如图所示的空间直角坐标系,则A(1,0,0),B(1,1,0),
P(0,1,m),C(0,1,0),
D(0,0,0),B1(1,1,2),D1(0,0,2).
所以
| BD |
B
|
| AP |
| AC |
又由
| AC |
| BD |
| AC |
B
|
| AC |
| B | 1 |
| D | 1 |
设AP与面BDD1B1所成的角为θ,
则sinθ=cos(
| π |
| 2 |
|
| ||||
|
|
| 2 | ||||||
|
| ||
| 2 |
解得m=
| ||
| 3 |
| ||
| 3 |
直线AP与平面BDD1B1所成角为60°;(5分)
(2)若在A1C1上存在这样的点Q,设此点的横坐标为x,
则Q(x,1-x,2),
| D1Q |
依题意,对任意的m要使D1Q在平面APD1上的射影垂直于AP.等价于
| D1Q |
| AP |
| D1Q |
| AP |
| 1 |
| 2 |
即Q为A1C1的中点时,满足题设的要求.(10分)
点评:本题主要考查了直线与平面之间的位置关系,考查空间想象能力、运算能力和推理论证能力,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
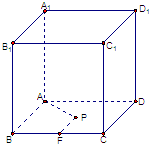 如图:在底面边长为1的正四棱柱ABCD-A1B1C1D1中,P为底面ABCD所在平面内一动点,点P到直线BC的距离等于它到直线AA1的距离,则P点的轨迹方程是( )
如图:在底面边长为1的正四棱柱ABCD-A1B1C1D1中,P为底面ABCD所在平面内一动点,点P到直线BC的距离等于它到直线AA1的距离,则P点的轨迹方程是( )
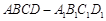 中,P是侧棱
中,P是侧棱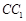 上的一点,
上的一点,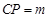 . (1)试确定m,使直线AP与平面BDD1B1所成角为60º;(2)在线段
. (1)试确定m,使直线AP与平面BDD1B1所成角为60º;(2)在线段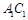 上是否存在一个定点
上是否存在一个定点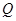 ,使得对任意的m,
,使得对任意的m,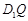 ⊥AP,并证明你的结论.
⊥AP,并证明你的结论. 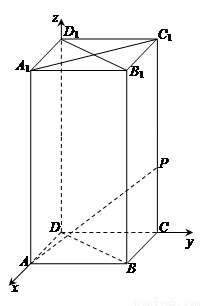
 中,P是侧棱
中,P是侧棱 上的一点,
上的一点, .
. 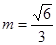 时,求直线AP与平面BDD1B1所成角的度数;
时,求直线AP与平面BDD1B1所成角的度数;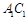 上是否存在一个定点
上是否存在一个定点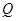 ,使得对任意的m,
,使得对任意的m,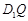 ⊥AP,并证明你的结论.
⊥AP,并证明你的结论. 