题目内容
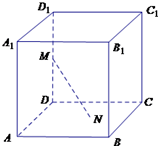
已知正方体ABCD-A′B′C′D′中，点E、F分别是棱BB′与面对角线B′D′的中点，求证：直线EF⊥直线A′D．
如图设正方体的棱长为：2，
所以A′（0，0，0），D（0，2，2），E（2，0，1），F（1，1，0），
所以
=（-1，1，-1），
=（0，2，2）
所以
•
=0+2-2=0．
所以
⊥
，
所以直线EF⊥直线A′D．
所以A′（0，0，0），D（0，2，2），E（2，0，1），F（1，1，0），
所以
| EF |
| A′D |
所以
| EF |
| A′D |
所以
| EF |
| A′D |
所以直线EF⊥直线A′D．
练习册系列答案
长江作业本同步练习册系列答案
小天才课时作业系列答案
一课四练系列答案
黄冈小状元满分冲刺微测验系列答案
相关题目
