题目内容
已知点 是直线
是直线
 上一动点,
上一动点,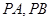 是圆C:
是圆C: 的两条切线,A、B是切点,若四边形
的两条切线,A、B是切点,若四边形 的最小面积是2,则
的最小面积是2,则 的值为?
的值为?
 .
.
解析试题分析:利用切线的性质,建立四边形PACB的面积与切线长PA的关系式,根据四边形PACB面积的最小值可以得到PA的最小值,再利用PA与CP之间的关系可以得到CP的最小值,而CP的最小值即圆心C到直线的距离,从而可以建立关于k的方程求得k的值.
C: ,圆心
,圆心 ,半径为1; 2分
,半径为1; 2分
如图,∵ ,∴
,∴ 4分
4分
∵ ,
, 6分
6分
又∵ ,∴
,∴
即点C到直线的距离为 8分
8分
∴ , 11分
, 11分
解得: (负舍) 12分
(负舍) 12分
∴ 13分
13分
考点:1、直线与圆的位置关系;2、点到直线的距离公式.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
 相切
相切 被圆C所截得的弦AB的长.
被圆C所截得的弦AB的长. 的圆经过点
的圆经过点 .
. 的标准方程;
的标准方程; 过点
过点 且被圆
且被圆 ,求直线
,求直线 ,使得以
,使得以 ,半径小于5.
,半径小于5. +y2=1.过
+y2=1.过 轴上的动点
轴上的动点 (m,0)作圆x2+y2=1的切线l交椭圆G于A,B两点.
(m,0)作圆x2+y2=1的切线l交椭圆G于A,B两点. 的最大距离;
的最大距离;  时,求A,B两点坐标;
时,求A,B两点坐标; 和
和 ,且圆心C在直线
,且圆心C在直线 :
: 上,求圆心为C的圆的标准方程.
上,求圆心为C的圆的标准方程. 是椭圆
是椭圆 上两点,点M的坐标为
上两点,点M的坐标为 .
. 轴对称,且
轴对称,且 为等边三角形时,求
为等边三角形时,求 的长;
的长; 内有一点
内有一点 ,
, 为过点
为过点 且倾斜角为
且倾斜角为 的弦.
的弦.
 时,求
时,求 ;
; ,求点
,求点
 (θ为参数)没有公共点,
(θ为参数)没有公共点,