题目内容

4．已知函数f（x）=$\frac{3x+2}{x+a}$（x≠-a，a≠$\frac{2}{3}$）
（1）求反函数f-1（x）；
（2）求使得f（x）=f-1（x）的a的值．

分析 （1）由函数y的解析式求出x的解析式，再把x、y互换，即可求得原函数的反函数．
（2）直接利用条件求出a的值．

解答 解：（1）由函数y=f（x）=$\frac{3x+2}{x+a}$（x≠-a，a≠$\frac{2}{3}$），可得x=$\frac{ay-2}{3-y}$，
故函数的反函数为f-1（x）=$\frac{ax-2}{3-x}$（x≠3）．
（2）由f（x）=f-1（x），可得$\frac{3x+2}{x+a}$=$\frac{ax-2}{3-x}$，可得a=-3．

点评 本题主要考查求一个函数的反函数的方法，属于基础题．

练习册系列答案
相关题目
14．一个几何体的三视图如图所示，则该几何体的体积$\frac{2}{3}π$．
15．向量$\overrightarrow{a}$，$\overrightarrow{b}$满足|$\overrightarrow{a}$|=1，|$\overrightarrow{b}$|=$\sqrt{2}$，（$\overrightarrow{a}$+$\overrightarrow{b}$）⊥（2$\overrightarrow{a}$-$\overrightarrow{b}$），则向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为90°．
12．已知$\frac{1}{3}$≤k＜1，函数f（x）=|2x-1|-k的零点分别为x1，x2（x1＜x2），函数g（x）=|2x-1|-$\frac{k}{2k+1}$的零点分别为x3，x4（x3＜x4），则（x4-x3）+（x2-x1）的最小值是log23．
19．已知集合A={x|x2-3x+2≥0}，B={x|m＜x＜m+1}，若B⊆A，求m的取值范围．
9．已知圆x2+y2=r2（r＞0）与抛物线y2=2$\sqrt{2}$x交于A、B两点，O是坐标原点，若OA⊥OB，则r的值为4．
16．求由抛物线f（x）=x2，直线x=0，x=1以及x轴所围成的平面图形的面积时，若将区间[0，1]5等分，以小区间中点的纵坐标为高，所有小矩形的面积之和为0.33．
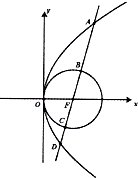15．已知抛物线G的顶点在原点，焦点F为圆（x-1）2+y2=1的圆心．设过点F的直线与抛物线G及圆F依次交于如图中所示的A，B，C，D四点．
（Ⅰ）求抛物线G的标准方程；
（Ⅱ）证明：|AB|•|CD|为定值；
（Ⅲ）若已知|AD|=a，试用a表示△AOD的面积S△AOD．
16．已知点A（2，1），抛物线y2=4x的焦点F，P是抛物线上的一动点则|PA|+|PF|的最小值为（　　）
A．1B．2C．3D．4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网