题目内容
15.向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=$\sqrt{2}$,($\overrightarrow{a}$+$\overrightarrow{b}$)⊥(2$\overrightarrow{a}$-$\overrightarrow{b}$),则向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为90°.分析 由向量垂直的条件可得($\overrightarrow{a}$+$\overrightarrow{b}$)•(2$\overrightarrow{a}$-$\overrightarrow{b}$)=0,根据向量数量积的运算化简得$\overrightarrow{a}•\overrightarrow{b}$=0,即可求出向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角.
解答 解:因为|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=$\sqrt{2}$,($\overrightarrow{a}$+$\overrightarrow{b}$)⊥(2$\overrightarrow{a}$-$\overrightarrow{b}$),
所以($\overrightarrow{a}$+$\overrightarrow{b}$)•(2$\overrightarrow{a}$-$\overrightarrow{b}$)=2${\overrightarrow{a}}^{2}$+$\overrightarrow{a}•$$\overrightarrow{b}$-${\overrightarrow{b}}^{2}$=0,
则2+$\overrightarrow{a}•$$\overrightarrow{b}$-2=0,即$\overrightarrow{a}•\overrightarrow{b}$=0,
所以$\overrightarrow{a}⊥\overrightarrow{b}$,则向量$\overrightarrow{a}$与$\overrightarrow{b}$的夹角为90°,
故答案为:90°.
点评 本题重点考查了向量数量积的运算,以及向量垂直的条件,属于中档题.

| A. | 若a2+b2≠0,则a≠0且b≠0 | B. | 若a2+b2≠0,则a≠0或b≠0 | ||
| C. | 若a≠0且b≠0,则a2+b2≠0 | D. | 若a≠0或b≠0,则a2+b2≠0 |
| A. | 10 | B. | 9 | C. | 8 | D. | 7 |
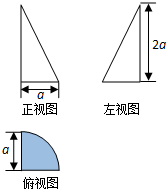
| A. | $\frac{2π{a}^{3}}{3}$ | B. | $\frac{π{a}^{3}}{3}$ | C. | πa3 | D. | $\frac{π{a}^{3}}{6}$ |
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
| A. | -i | B. | i | C. | 1-i | D. | 1+i |