Question

15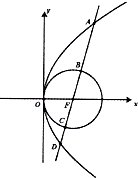．已知抛物线G的顶点在原点，焦点F为圆（x-1）²+y²=1的圆心．设过点F的直线与抛物线G及圆F依次交于如图中所示的A，B，C，D四点．
（Ⅰ）求抛物线G的标准方程；
（Ⅱ）证明：|AB|•|CD|为定值；
（Ⅲ）若已知|AD|=a，试用a表示△AOD的面积S_△AOD．

Answer 1

分析 （Ⅰ）设抛物线方程为y²=2px，（p＞0），由圆心可得F的坐标，进而得到抛物线的方程；
（Ⅱ）设A（x₁，y₁），D（x₂，y₂），由抛物线的定义可得，|AF|=x₁+1，|DF|=x₂+1，若直线AD斜率存在，设AD的方程，代入抛物线方程，运用韦达定理，即可求得所求之积；若直线AD斜率不存在，求出AD的方程，即可求得所求值；
（Ⅲ）若直线AD斜率存在，求出O到AD的距离d，运用S_△AOD=$\frac{1}{2}$d•|AD|，计算即可得到面积；当直线AD斜率不存在，易得所求面积．

解答 （Ⅰ）解：设抛物线方程为y²=2px，（p＞0），
焦点F为圆（x-1）²+y²=1的圆心，即有F（1，0），
则p=2，抛物线方程为y²=4x；
（Ⅱ）证明：抛物线的准线为x=-1，设A（x₁，y₁），D（x₂，y₂），
由抛物线的定义可得，|AF|=x₁+1，|DF|=x₂+1，
|AB|=|AF|-|BF|=x₁+1-1=x₁，同理|CD|=x₂，
若直线AD斜率存在，设AD：y=k（x-1），（k≠0），
代入抛物线方程，可得k²x²-（2k²+4）x+k²=0，
x₁+x₂=2+$\frac{4}{{k}^{2}}$，x₁x₂=1，
则|AB|•|CD|=x₁x₂=1．
若若直线AD斜率不存在，则AD：x=1，此时x₁=x₂=1，即有|AB|•|CD|=1．
综上可得，|AB|•|CD|为定值1．
（Ⅲ）解：若直线AD斜率存在，则|AD|=|AF|+|DF|=x₁+x₂+2=4+$\frac{4}{{k}^{2}}$=a，
即有$\frac{|k|}{\sqrt{1+{k}^{2}}}$=$\frac{2}{\sqrt{a}}$，
由O到直线AD的距离d=$\frac{|k|}{\sqrt{1+{k}^{2}}}$=$\frac{2}{\sqrt{a}}$，
S_△AOD=$\frac{1}{2}$d•|AD|=$\frac{1}{2}$$•\frac{2}{\sqrt{a}}$•a=$\sqrt{a}$，
当直线AD斜率不存在，则x₁=x₂=1，|AD|=x₁+x₂+2=4，a=4，
S_△AOD=$\frac{1}{2}$×1×4=2=$\sqrt{a}$．
综上可得，△AOD的面积S_△AOD=$\sqrt{a}$．

点评 本题考查抛物线的定义、方程和性质，主要考查直线和抛物线方程联立，运用韦达定理，以及点到直线的距离公式，注意直线斜率不存在的情况，属于中档题．