Question

10．已知g（x）=x（2-x）（0＜x＜1），g（1）=0，若函数y=f（x）（x∈R）是以2为周期的奇函数，且在[0，1]上f（x）=g（x），画出y=f（x）（-2≤x≤2）的图象并求其表达式．

Answer 1

分析 根据函数的奇偶性和周期性的关系求出函数的解析式即可．

解答 解：∵在[0，1]上f（x）=g（x），
∴当0＜x＜1时，f（x）=g（x）=x（2-x），
当x=1时，f（1）=g（1）=0，
∵y=f（x）（x∈R）是以2为周期的奇函数，
∴当x=0时，f（0）=0，
当x=-1时，f（-1）=-f（1）=0．
当x=2时，f（2）=f（0）=0，
若-1＜x＜0，则0＜-x＜1，
此时f（-x）=-x（2+x）=-f（x），
∴f（x）=x（2+x），-1＜x＜0，
若1＜x＜2，则-1＜x-2＜0，
则f（x）=f（x-2）=（x-2）x，1＜x＜2，
若-2＜x＜-1，则1＜-x＜2，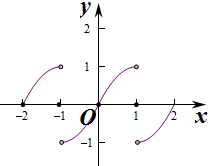
则f（-x）=-x（-x-2）=-f（x），
即f（x）=-x（x+2），-2＜x＜-1
综上：f（x）=$\left\{\begin{array}{l}{-x（x+2），}&{-2≤x＜-1}\\{x（2+x），}&{-1＜x≤0}\\{x（2-x），}&{0＜x＜1}\\{x（x-2），}&{1＜x≤2}\\{0}&{x=±1}\end{array}\right.$，
对应的图象为：

点评 本题主要考查函数解析式的求解，利用函数的奇偶性和周期性是解决本题的关键．