题目内容
【题目】在平面直角坐标系![]() 中,设动点
中,设动点![]() 到两定点
到两定点![]() ,
, ![]() 的距离的比值为
的距离的比值为![]() 的轨迹为曲线
的轨迹为曲线![]() .
.
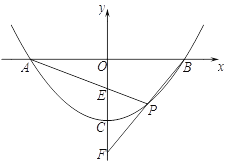
(Ⅰ)求曲线![]() 的方程;
的方程;
(Ⅱ)若直线![]() 过点
过点![]() ,且点
,且点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求直线
,求直线![]() 的方程,并判断直线
的方程,并判断直线![]() 与曲线
与曲线![]() 的位置关系.
的位置关系.
【答案】(Ⅰ)![]() (Ⅱ)见解析
(Ⅱ)见解析
【解析】试题分析:(Ⅰ)设![]() 为所求曲线
为所求曲线![]() 上任意一点,由题意得,
上任意一点,由题意得, ![]() .又
.又![]() ,
, ![]() ,所以
,所以![]() ,化简得
,化简得![]() ,即得出曲线
,即得出曲线![]() 的方程;
的方程;
(Ⅱ)当直线![]() 的斜率不存在时,不符合题意.设直线
的斜率不存在时,不符合题意.设直线![]() 的方程为
的方程为![]() ,因为点
,因为点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,即
,即![]() ,解得
,解得![]() .即得出直线
.即得出直线![]() 的方程,利用圆心
的方程,利用圆心![]() 到直线
到直线![]() 的距离与半径关系得出直线
的距离与半径关系得出直线![]() 与曲线
与曲线![]() 的位置关系.
的位置关系.
试题解析:
(Ⅰ)设![]() 为所求曲线
为所求曲线![]() 上任意一点,由题意得,
上任意一点,由题意得, ![]() .又
.又![]() ,
, ![]() ,所以
,所以![]() ,化简得
,化简得![]() .故曲线
.故曲线![]() 的方程为
的方程为![]() .
.
(Ⅱ)当直线![]() 的斜率不存在时,不符合题意.设直线
的斜率不存在时,不符合题意.设直线![]() 的方程为
的方程为![]() ,因为点
,因为点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,即
,即![]() ,解得
,解得![]() .所以直线
.所以直线![]() 的方程为
的方程为![]() ,即
,即![]() .因为圆心
.因为圆心![]() 到直线
到直线![]() 的距离为
的距离为![]() (半径),所以直线
(半径),所以直线![]() 与曲线
与曲线![]() 相交.
相交.

练习册系列答案
 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案
相关题目