题目内容
若直线y=a与函数f（x）=x3-3x的图象有三个不同的交点，则a∈______．
∵函数f（x）=x3-3 x
∴f′（x）=3x2-3
令f′（x）=0，可解得x=±1，
即函数f（x）=x3-3x的极值分别为f（1）=-2，f（-1）=2，如图
符合题意的参数的a的取值范围是（-2，2）
故答案为：（-2，2）
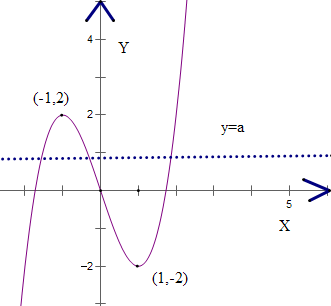
∴f′（x）=3x2-3
令f′（x）=0，可解得x=±1，
即函数f（x）=x3-3x的极值分别为f（1）=-2，f（-1）=2，如图
符合题意的参数的a的取值范围是（-2，2）
故答案为：（-2，2）
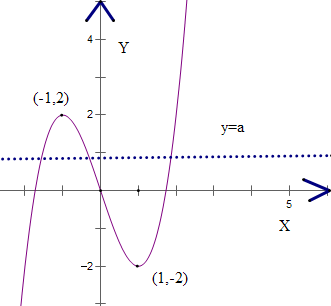
练习册系列答案
阅读快车系列答案
相关题目
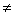0)有一个零点是－2，则函数g(x)＝bx2－ax的零点是（ ）
