题目内容
【题目】如图,圆![]() ,
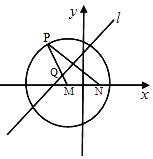
,![]() 是圆M内一个定点,P是圆上任意一点,线段PN的垂直平分线l和半径MP相交于点Q,当点P在圆M上运动时,点Q的轨迹为曲线E
是圆M内一个定点,P是圆上任意一点,线段PN的垂直平分线l和半径MP相交于点Q,当点P在圆M上运动时,点Q的轨迹为曲线E
(1)求曲线E的方程;
(2)过点D(0,3)作直线m与曲线E交于A,B两点,点C满足![]() (O为原点),求四边形OACB面积的最大值,并求此时直线m的方程;
(O为原点),求四边形OACB面积的最大值,并求此时直线m的方程;
(3)已知抛物线![]() 上,是否存在直线与曲线E交于G,H,使得G,H的中点F落在直线y=2x上,并且与抛物线相切,若直线存在,求出直线的方程,若不存在,说明理由.
上,是否存在直线与曲线E交于G,H,使得G,H的中点F落在直线y=2x上,并且与抛物线相切,若直线存在,求出直线的方程,若不存在,说明理由.
【答案】(1)![]() (2)2,
(2)2,![]() (3)存在,x+8y﹣8=0或x=0
(3)存在,x+8y﹣8=0或x=0
【解析】
(1)由已知可得|QN|=|QP|,进而有|QM|+|QP|=4>|MN|,根据椭圆定义,即可求解;
(2)由![]() ,四边形OACB为平行四边形,设
,四边形OACB为平行四边形,设![]() ,
,![]() ,设直线
,设直线![]() 斜率为
斜率为![]() (斜率不存在另讨论),求出直线
(斜率不存在另讨论),求出直线![]() 方程,与椭圆方程联立,消元,求出
方程,与椭圆方程联立,消元,求出![]() 的范围,根据韦达定理得出,
的范围,根据韦达定理得出,![]() 关系,进而将
关系,进而将![]() 表示是为
表示是为![]() 的目标函数,换元,利用基本不等式,即可求解;
的目标函数,换元,利用基本不等式,即可求解;
(3)若直线斜率不存在,![]() 满足条件,若斜率存在,设直线与曲线E的交点坐标为
满足条件,若斜率存在,设直线与曲线E的交点坐标为![]() ,应用点差法,结合G,H的中点F落在直线y=2x上,求出直线
,应用点差法,结合G,H的中点F落在直线y=2x上,求出直线![]() 的斜率,设直线方程,与抛物线方程联立,利用
的斜率,设直线方程,与抛物线方程联立,利用![]() ,求出直线
,求出直线![]() 方程,验证直线
方程,验证直线![]() 与椭圆是否相交,即可求解.
与椭圆是否相交,即可求解.
(1)由题意可知,Q在PN的垂直平分线上,所以|QN|=|QP|,
又因为|QM|+|QP|=r=4,所以|QM|+|QP|=4>|MN|,
所以Q点的轨迹为椭圆,且2a=4即a=2,
由题意可知c=![]() ,所以b=1,
,所以b=1,
∴曲线E的方程为![]()
(2)因为![]() ,所以四边形OACB为平行四边形,
,所以四边形OACB为平行四边形,
当直线m的斜率不存在时,显然不符合题意;
当直线m的斜率存在时,设直线 的方程为y=kx+3,
直线m与曲线E交于A(x1,y1),B(x2,y2)两点,
联立方程组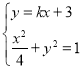 ,消去y,
,消去y,
整理得(1+4k2)x2+24kx+32=0.由△=(24k)2﹣128(1+4k2)>0
得k2>2. x1+x2=﹣![]() ,x1x2=
,x1x2=![]() ,
,
因为S△OAB=![]() |OD||x1﹣x2|=
|OD||x1﹣x2|=![]() |x1﹣x2|,
|x1﹣x2|,
所以SOACB=2S△OAB=3|x1﹣x2|=3![]()
=3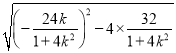 =24
=24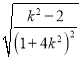 ,
,
令k2﹣2=t,则k2=t+2(由上式知t>0),
所以SOANB=24![]() =24
=24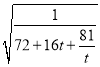 ≤24
≤24![]() =2,
=2,
当且仅当t=![]() ,即k2=
,即k2=![]() 时取等号,∴当k=±
时取等号,∴当k=±![]() 时,
时,
平行四边形OACB的面积的最大值为2.此时直线的方程为y=±![]() x+3
x+3
(3)若直线斜率存在,设直线与曲线E的交点坐标为![]() ,
,
满足曲线E的方程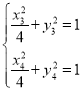 ,两式作差可得
,两式作差可得![]() ,
,
G,H的中点F落在直线y=2x上,
则有![]() 代入可得
代入可得![]() ,
,
直线方程可以设为![]() 与抛物线方程联立,
与抛物线方程联立,
得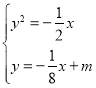 ,消元可得方程
,消元可得方程![]() ,
,
直线与抛物线相切则有![]() ,所以
,所以![]() ,
,
则直线的方程为x+8y﹣8=0,与椭圆方程联立: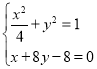 ,
,
消元可得方程17y2﹣32y+15=0,△=322﹣4×17×15>0,
所以直线x+8y﹣8=0满足题意.
若直线斜率不存在时,直线x=0满足题意.
所以,综上这样的直线存在,方程是x+8y﹣8=0或x=0.

 名校课堂系列答案
名校课堂系列答案