题目内容
已知椭圆C的中心在原点,焦点在x轴上,它的一个顶点B恰好是抛物线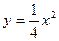 的焦点,
的焦点,
离心率等于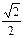 .直线
.直线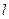 与椭圆C交于
与椭圆C交于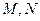 两点.
两点.
(Ⅰ)求椭圆C的方程;
(Ⅱ) 椭圆C的右焦点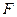 是否可以为
是否可以为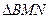 的垂心?若可以,求出直线
的垂心?若可以,求出直线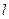 的方程;
的方程;
若不可以,请说明理由.
解:(1)设C方程为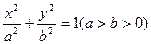 ,则b = 1.
,则b = 1.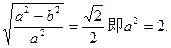
∴椭圆C的方程为 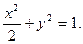 ………………4分
………………4分
(Ⅱ)假设存在直线 ,使得点
,使得点 是
是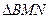 的垂心.
的垂心.
易知直线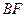 的斜率为
的斜率为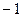 ,从而直线
,从而直线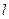 的斜率为1.
的斜率为1.
设直线的方程为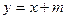 , ………………6分
, ………………6分
代入椭圆方程并整理,可得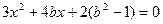 .
.
设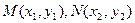 ,则
,则 ,
,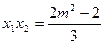 .
.
于是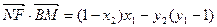
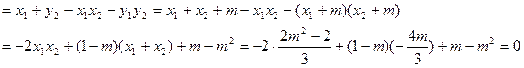
解之得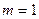 或
或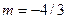 . ………………10分
. ………………10分
当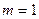 时,点
时,点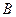 即为直线
即为直线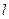 与椭圆的交点,不合题意.
与椭圆的交点,不合题意.
当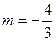 时,经检验知
时,经检验知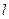 和椭圆相交,符合题意.
和椭圆相交,符合题意.
所以,当且仅当直线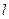 的方程为
的方程为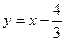 时, 点
时, 点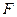 是
是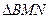 的垂心
的垂心
解析

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在极坐标系中,直线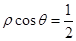 与曲线
与曲线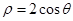 相交于
相交于 两点,
两点,  为极点,则
为极点,则 的大小为( ).
的大小为( ).
A.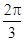 | B.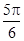 | C.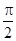 | D.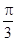 |
 的离心率为
的离心率为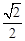 ,其中左焦点F(-2,0).
,其中左焦点F(-2,0).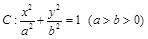 的左、右焦点分别为
的左、右焦点分别为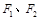 ,上顶点为
,上顶点为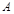 ,离心率为
,离心率为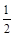 ,在
,在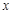 轴负半轴上有一点
轴负半轴上有一点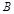 ,且
,且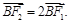
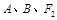 三点的圆恰好与直线
三点的圆恰好与直线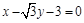 相切,求椭圆C的方程;
相切,求椭圆C的方程; 作斜率为
作斜率为 的直线
的直线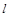 与椭圆C交于
与椭圆C交于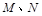 两点,在
两点,在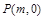 ,使得以
,使得以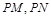 为邻边的平行四边形是菱形,如果存在,求出
为邻边的平行四边形是菱形,如果存在,求出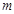 的取值范围;如果不存在,说明理由.
的取值范围;如果不存在,说明理由.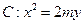
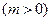 和直线
和直线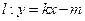 没有公共点(其中
没有公共点(其中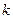 、
、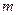 为常数),动点
为常数),动点 是直线
是直线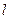 上的任意一点,过
上的任意一点,过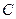 的两条切线,切点分别为
的两条切线,切点分别为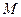 、
、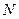 ,且直线
,且直线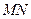 恒过点
恒过点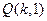 .
. 点为原点,连结
点为原点,连结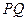 交抛物线
交抛物线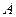 、
、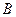 两点,
两点,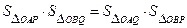
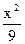 +
+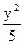 =1的焦点F1、F2,在直线l:x+y-6=0上找一点M,求以F1、F2为焦点,通过点M且长轴最短的椭圆方程.
=1的焦点F1、F2,在直线l:x+y-6=0上找一点M,求以F1、F2为焦点,通过点M且长轴最短的椭圆方程.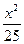 +
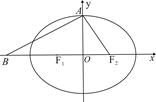
+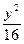 =1上任意一点,F1、F2为左、右焦点,如图所示.
=1上任意一点,F1、F2为左、右焦点,如图所示.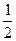 |PF1|;
|PF1|; ·
·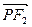 =0,若存在,求出P点的坐标, 若不存在,试说明理由
=0,若存在,求出P点的坐标, 若不存在,试说明理由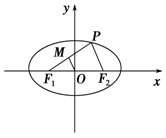
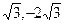 ),
),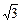 ,求椭圆的方程.
,求椭圆的方程.