题目内容
(本题满分14分)已知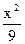 +
+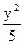 =1的焦点F1、F2,在直线l:x+y-6=0上找一点M,求以F1、F2为焦点,通过点M且长轴最短的椭圆方程.
=1的焦点F1、F2,在直线l:x+y-6=0上找一点M,求以F1、F2为焦点,通过点M且长轴最短的椭圆方程.
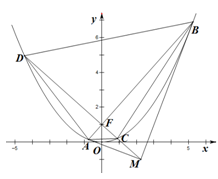
解:由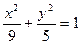 ,得F1(2,0),F2(-2,0) (3分)
,得F1(2,0),F2(-2,0) (3分)
F1关于直线l的对称点F1/(6,4) (4分)
,连F1/F2交l于一点,即为所求的点M,∴2a=|MF1|+|MF2|=|F1/F2|=4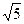 ,a=2
,a=2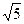 (4分)
(4分)
∴,又c=2,∴b2=16, (4分)
故所求椭圆方程为 . (3分)
. (3分)
解析

练习册系列答案
相关题目
曲线的极坐标方程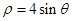 化为直角坐标为( )
化为直角坐标为( )
A. | B.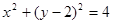 |
C.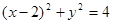 | D.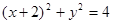 |
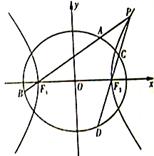
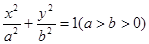 的离心率为
的离心率为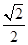 ,以该椭圆上的点和椭圆的左、右焦点
,以该椭圆上的点和椭圆的左、右焦点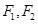 为顶点的三角形的周长为
为顶点的三角形的周长为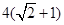 .一等轴双曲线的顶点是该椭圆的焦点,设
.一等轴双曲线的顶点是该椭圆的焦点,设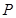 为该双曲线上异于顶点的任一点,直线
为该双曲线上异于顶点的任一点,直线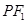 和
和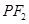 与椭圆的交点分别为
与椭圆的交点分别为 和
和 .
.
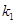 、
、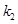 ,证明
,证明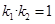 ;
;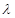 ,使得
,使得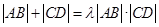 恒成立?若存在,求
恒成立?若存在,求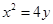 的焦点为
的焦点为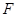 ,过焦点
,过焦点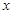 轴的动直线
轴的动直线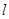 交抛物线于
交抛物线于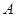 ,
,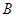 两点,抛物线在
两点,抛物线在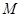 .
.

 交该抛物线于
交该抛物线于 ,
, 两点,求四边形
两点,求四边形 面积的最小值.
面积的最小值.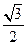 ,已知点P(0,
,已知点P(0,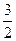 )到这个椭圆上的点的最远距离是
)到这个椭圆上的点的最远距离是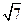 ,求这个椭圆的方程。
,求这个椭圆的方程。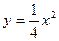 的焦点,
的焦点,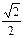 .直线
.直线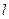 与椭圆C交于
与椭圆C交于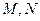 两点.
两点.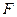 是否可以为
是否可以为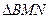 的垂心?若可以,求出直线
的垂心?若可以,求出直线 是圆
是圆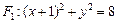 上任意一点,点
上任意一点,点 与点
与点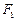 关于原点对称。线段
关于原点对称。线段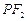 的中垂线
的中垂线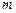 分别与
分别与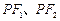 交于
交于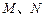 两点.
两点.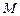 的轨迹
的轨迹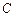 的方程;
的方程; 的直线
的直线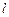 与曲线
与曲线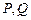 两点,若
两点,若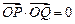 (
(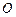 为坐标原点),试求直线
为坐标原点),试求直线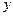 轴
轴 上截距的取值范围.
上截距的取值范围.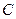 的方程为
的方程为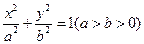 ,点
,点 分别为其左、右顶点,点
分别为其左、右顶点,点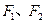 分别为其左、右焦点,以点
分别为其左、右焦点,以点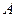 为圆心,
为圆心,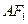 为半径作圆
为半径作圆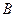 为圆心,
为圆心,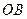 为半径作圆
为半径作圆 被圆
被圆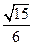 ;
;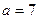 ,问是否存在点
,问是否存在点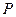 ,使得过
,使得过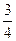 ;若存在,请求出所有的
;若存在,请求出所有的