题目内容
【题目】根据下列算法语句,将输出的A值依次记为a1 , a2 , …,an , …,a2015;已知函数f(x)=a2sin(ωx+φ)(ω>0,|φ|< ![]() )的最小正周期是a1 , 且函数y=f(x)的图象关于直线x=
)的最小正周期是a1 , 且函数y=f(x)的图象关于直线x= ![]() 对称.
对称.
(Ⅰ)求函数y=f(x)表达式;
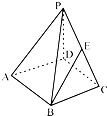
(Ⅱ)已知△ABC中三边a,b,c对应角A,B,C,a=4,b=4 ![]() ,∠A=30°,求f(B).
,∠A=30°,求f(B).
【答案】解:(Ⅰ)由已知,当n≥2时,an=1+3+5+…+(2n﹣1)=n2而a1=1也符合an=n2 , 知a1=1,a2=4,所以函数y=f(x)的最小正周期为1,所以ω=2π,
则f(x)=4sin(2πx+φ),
又函数y=f(x)的图象关于直线x= ![]() 对称
对称
所以 ![]() +φ=kπ+
+φ=kπ+ ![]() (k∈Z),因为|φ|<
(k∈Z),因为|φ|< ![]() ,所以φ=
,所以φ= ![]() ,则f(x)=4sin(2πx+
,则f(x)=4sin(2πx+ ![]() )
)
(Ⅱ)由正弦定理计算 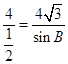 ,∴sinB=
,∴sinB= ![]() ,∴B为
,∴B为 ![]() 或
或 ![]() ,
,
可得f(B)=4sin( ![]() +
+ ![]() )或4sin(
)或4sin( ![]() +
+ ![]() )
)
【解析】(Ⅰ)由已知算法语句可知所求为2015个奇数的和;根据a1=1,a2=4,得到函数的周期,由对称轴x= ![]() ,结合|φ|<
,结合|φ|< ![]() 得到φ,从而求出三角函数解析式;(Ⅱ)由正弦定理计算B,即可求f(B).
得到φ,从而求出三角函数解析式;(Ⅱ)由正弦定理计算B,即可求f(B).

 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案【题目】某公司为确定下一年度投入某种产品的宣传费,需了解年宣传费![]() (单位:千元)对年销售量
(单位:千元)对年销售量![]() (单位:t)和年利润
(单位:t)和年利润![]() (单位:千元)的影响.对近8年的年宣传费
(单位:千元)的影响.对近8年的年宣传费![]() 和年销售量
和年销售量![]() (i=1,2,…,8)数据作了初步处理,得到右面的散点图及一些统计量的值.
(i=1,2,…,8)数据作了初步处理,得到右面的散点图及一些统计量的值.

|
|
|
|
|
|
|
46.6 | 563 | 6.8 | 289.8 | 1.6 | 1469 | 108.8 |
表中![]() ,
, ![]()
(1)根据散点图判断, ![]() 与
与![]() 哪一个适宜作为年销售量
哪一个适宜作为年销售量![]() 关于年宣传费
关于年宣传费![]() 的回归方程类型?(给出判断即可,不必说明理由)
的回归方程类型?(给出判断即可,不必说明理由)
(2)根据(1)的判断结果及表中数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
(3)已知这种产品的年利润![]() 与
与![]() 的关系为
的关系为![]() .根据(2)的结果回答下列问题:
.根据(2)的结果回答下列问题:
①年宣传费![]() =49时,年销售量及年利润的预报值是多少?
=49时,年销售量及年利润的预报值是多少?
②年宣传费![]() 为何值时,年利润的预报值最大?
为何值时,年利润的预报值最大?
附:对于一组数据![]() ,
, ![]() …,
…,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为
![]()