题目内容
(本小题满分12分)已知椭圆C:
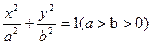 的左、右顶点的坐标分别为
的左、右顶点的坐标分别为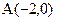 ,
,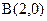 ,离心率
,离心率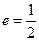 。
。(Ⅰ)求椭圆C的方程:
(Ⅱ)设椭圆的两焦点分别为
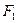 ,
,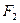 ,若直线
,若直线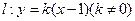 与椭圆交于
与椭圆交于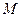 、
、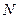 两点,证明直线
两点,证明直线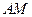 与直线
与直线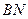 的交点在直线
的交点在直线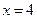 上。
上。(1)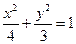
(2)将直线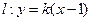 代入椭圆C的方程
代入椭圆C的方程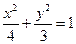 并整理.
并整理.
得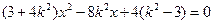 .
.
设直线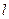 与椭圆C交点
与椭圆C交点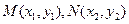 ,
,
由根系数的关系,得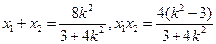 .
.
直线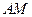 的方程为:
的方程为: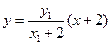 ,它与直线
,它与直线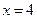 的交点坐标为
的交点坐标为
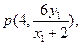 同理可求得直线
同理可求得直线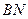 与直线
与直线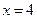 的交点坐标为
的交点坐标为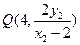 .
.
下面证明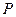 、
、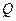 两点重合,即证明
两点重合,即证明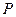 、
、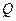 两点的纵坐标相等:
两点的纵坐标相等:
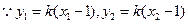 ,
,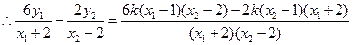
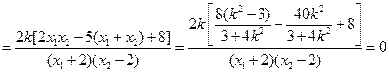
因此结论成立.
综上可知.直线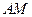 与直线
与直线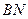 的交点住直线
的交点住直线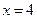 上.
上.
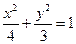
(2)将直线
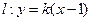 代入椭圆C的方程
代入椭圆C的方程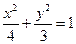 并整理.
并整理.得
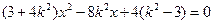 .
.设直线
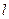 与椭圆C交点
与椭圆C交点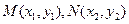 ,
,由根系数的关系,得
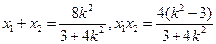 .
. 直线
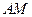 的方程为:
的方程为: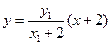 ,它与直线
,它与直线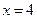 的交点坐标为
的交点坐标为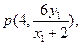 同理可求得直线
同理可求得直线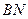 与直线
与直线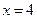 的交点坐标为
的交点坐标为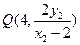 .
.下面证明
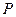 、
、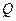 两点重合,即证明
两点重合,即证明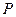 、
、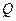 两点的纵坐标相等:
两点的纵坐标相等: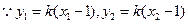 ,
,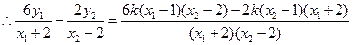
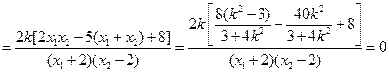
因此结论成立.
综上可知.直线
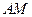 与直线
与直线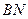 的交点住直线
的交点住直线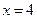 上.
上.略

练习册系列答案
相关题目
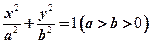 的左、右焦点分别为
的左、右焦点分别为 ,过
,过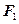 的直线
的直线 与椭圆交于
与椭圆交于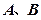 两点。
两点。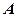 在圆
在圆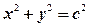 (
(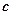 为椭圆的半焦距)上,且
为椭圆的半焦距)上,且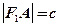 ,求椭圆的离心率;
,求椭圆的离心率; (Ⅱ)若函数
(Ⅱ)若函数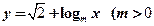 且
且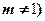 的图象,无论
的图象,无论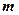 为何值时恒过定点
为何值时恒过定点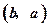 ,求
,求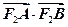 的取值范围。
的取值范围。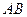 ). 某园林公司承接了该中心花园的施工建设,
). 某园林公司承接了该中心花园的施工建设,
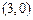 是椭圆C的一个焦点,
是椭圆C的一个焦点, 且椭圆C上的点
且椭圆C上的点 到点F的最大距离为8
到点F的最大距离为8 ;
;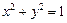 ,直线
,直线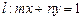 . 求当点
. 求当点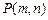 在椭圆C上运动时,直线
在椭圆C上运动时,直线 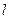 被圆O所截得的弦长的取值范围.
被圆O所截得的弦长的取值范围.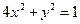 及直线
及直线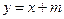 .
.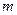 的取值范围.
的取值范围. 的焦点为F1,F
的焦点为F1,F 2,P为椭圆上一点,若
2,P为椭圆上一点,若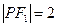 ,则
,则 ( )
( )
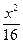 +
+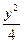 =1的右顶点是A,上下两个顶点分别为B、D,四边形DAMB是矩形(O为坐标原点)
=1的右顶点是A,上下两个顶点分别为B、D,四边形DAMB是矩形(O为坐标原点) ,点E、P分别是线段OA、AM的中点。
,点E、P分别是线段OA、AM的中点。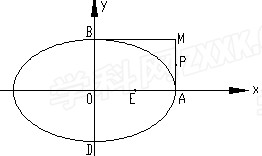
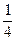 ,求证:直线RS过定点,并求出此定点的坐标。
,求证:直线RS过定点,并求出此定点的坐标。 ,过右焦点
,过右焦点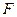 且
且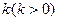 的直线与
的直线与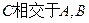 两点,若
两点,若 ,则
,则 ( )
( )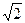
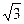
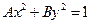 表示焦点在x轴上的椭圆,则
表示焦点在x轴上的椭圆,则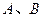 满足的条件是( )
满足的条件是( )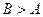
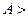
 ,且
,且