题目内容
(12分)如图7-4,已知△ABC中, ∠ACB=90°,CD⊥AB,且AD=1,BD=2,△ACD绕CD旋转至A′CD,使点A′与点B之间的距离A′B=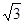 。
。
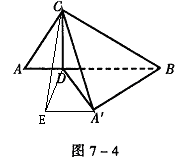
(1)求证:BA′⊥平面A′CD;
(2)求二面角A′-CD-B的大小;
(3)求异面直线A′C与BD所成的角的余弦值。
 。
。
(1)求证:BA′⊥平面A′CD;
(2)求二面角A′-CD-B的大小;
(3)求异面直线A′C与BD所成的角的余弦值。
解 (1)∵CD⊥AB,
∴CD⊥A′D,CD⊥DB,
∴CD⊥平面A′BD,
∴CD⊥BA′。
又在△A′DB中,A′D=1,DB=2,A′B=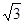 ,
,
∴∠BA′D=90°,即BA′⊥A′D,
∴BA′⊥平面A′CD。
(2)∵CD⊥DB,CD⊥A′D,
∴∠BDA′是二面角A′—CD—B的平面角。
又Rt△A′BD中,A′D=1,BD=2,
∴∠A′DB=60°,
即 二面角A′—CD—B为60°。
(3)过A′作A′E∥BD,在平面A′BD中作DE⊥A′E于E,连CE,则∠CA′E为A′C与BD所成角。
∵CD⊥平面A′BD,DE⊥A′E,∴A′E⊥CE。
∵EA′∥AB,∠A′DB=60°,∴∠DA′E=60°,
又A′D=1,∠DEA′=90°,
∴A′E=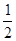
又∵在Rt△ACB中,AC=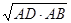 =
=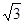
∴A′C=AC=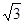
∴Rt△CEA′中,cos∠CA′E=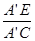 =
=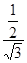 =
=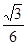 ,
,
即异面直线A′C与BD所成角的余弦值为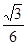 。
。
∴CD⊥A′D,CD⊥DB,
∴CD⊥平面A′BD,
∴CD⊥BA′。
又在△A′DB中,A′D=1,DB=2,A′B=
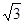 ,
,∴∠BA′D=90°,即BA′⊥A′D,
∴BA′⊥平面A′CD。
(2)∵CD⊥DB,CD⊥A′D,
∴∠BDA′是二面角A′—CD—B的平面角。
又Rt△A′BD中,A′D=1,BD=2,
∴∠A′DB=60°,
即 二面角A′—CD—B为60°。
(3)过A′作A′E∥BD,在平面A′BD中作DE⊥A′E于E,连CE,则∠CA′E为A′C与BD所成角。
∵CD⊥平面A′BD,DE⊥A′E,∴A′E⊥CE。
∵EA′∥AB,∠A′DB=60°,∴∠DA′E=60°,
又A′D=1,∠DEA′=90°,
∴A′E=
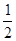
又∵在Rt△ACB中,AC=
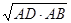 =
=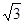
∴A′C=AC=
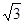
∴Rt△CEA′中,cos∠CA′E=
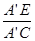 =
=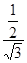 =
=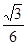 ,
,即异面直线A′C与BD所成角的余弦值为
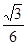 。
。略

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 的侧棱长和底面边长均为
的侧棱长和底面边长均为 ,
,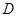 是
是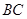 的中点.
的中点.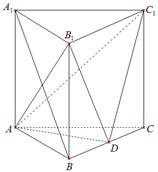
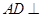 平面
平面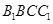 ;
; 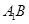 ∥平面
∥平面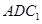 ;
;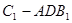 的体积.
的体积.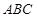 —
—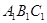 的底面边长为
的底面边长为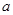 ,侧棱长为
,侧棱长为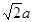 ,则
,则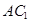 与侧面
与侧面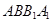 所成的角为( )
所成的角为( )
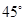

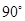
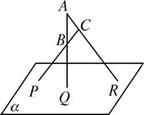
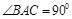 ,
,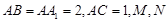 分别是
分别是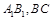 的中点。 (Ⅰ)证明:
的中点。 (Ⅰ)证明: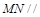 平面
平面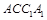 ;
;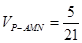 ,求
,求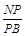 的值
的值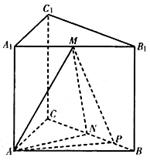
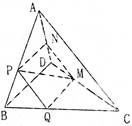
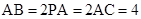 ,N为AB上一点且满足
,N为AB上一点且满足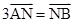 ,M,S分别为PB,BC的中点
,M,S分别为PB,BC的中点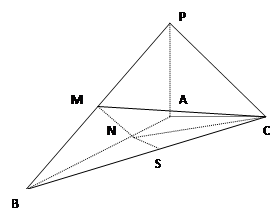
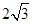 ,
,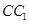 =
=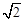 ,则二面角
,则二面角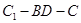 的大小为_______;
的大小为_______;