Question

【题目】如图，在直三棱柱ABC﹣A1B1C1中，AB=4，AC=BC=3，D为AB的中点

（1）求点C到平面A1ABB1的距离；
（2）若AB1⊥A1C，求二面角A1﹣CD﹣C1的平面角的余弦值．

Answer 1

【答案】
（1）解：由AC=BC，D为AB的中点，得CD⊥AB．又CD⊥AA1．

故CD⊥平面A1ABB1．

所以点C到平面A1ABB1的距离为CD= =

（2）解：[解法一]

如图1，取D1为A1B1的中点，连接DD1，则DD1∥AA1∥CC1．

又由（1）知CD⊥平面A1ABB1．故CD⊥A1D，CD⊥D1D，所以∠A1DD1为所求的二面角A1﹣CD﹣C1的平面角．因A1D为A1C在面A1ABB1中的射影，又已知AB1⊥A1C由三垂线定理的逆定理得AB1⊥A1D．从而∠A1AB1、∠A1DA都与∠B1AB互余．因此∠A1AB1=∠A1DA，所以Rt△A1AD∽Rt△B1A1A．因此AA1：AD=A1B1：AA1，即AA12=ADA1B1=8，得AA1=2 ，从而A1D= =2 ．所以Rt△A1D1D中，cos∠A1DD1= = =

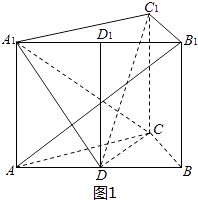
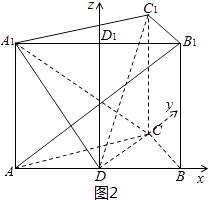
解法二：如图2，过D作DD1∥AA1交A1B1于D1，在直三棱柱中，有DB，DC，DD1两两垂直，以D为原点，射线DB，DC，DD1分别为X轴、Y轴、Z轴的正半轴建立空间直角坐标系D﹣xyz．

设直三棱柱的高为h，则A（﹣2，0，0），A1（﹣2，0，h），B1（2，0，h），C（0， ，0），C1（0， ，h），从而 =（4，0，h）， =（2， ，﹣h）

由AB1⊥A1C，可得8﹣h2=0，h=2 ，故 =（﹣2，0，2）， =（0，0，2 ）， =（0， ，0）

设平面A1CD的法向量为 =（x1，y1，z1），则有 ⊥ ， ⊥

∴ =0且 =0，即 ，取z1=1，则 =（ ，0，1）

设平面C1CD的法向量为 =（x2，y2，z2），则 ⊥ ， ⊥ ，即 且 =0，取x2=1，得 =（1，0，0），

所以cos＜ ， ＞= = = ，所以二面角A1﹣CD﹣C1span>的平面角的余弦值

【解析】（1）由题意，由于可证得CD⊥平面A1ABB1 ． 故点C到平面的距离即为CD的长度，易求；（2）解法一：由题意结合图象，可通过作辅助线先作出二面角的平面角∠A1DD1 ， 然后在直角三角形A1D1D中求出二面角的余弦；
解法二：根据几何体的形状，可过D作DD1∥AA1交A1B1于D1 ， 在直三棱柱中，可得DB，DC，DD1两两垂直，则以D为原点，射线DB，DC，DD1分别为X轴、Y轴、Z轴的正半轴建立空间直角坐标系D﹣xyz．给出各点的坐标，分别求出两平面的法向量，求出两向量的夹角即为两平面的夹角．