题目内容
【题目】已知a＞0，b∈R，函数f（x）=4ax3﹣2bx﹣a+b．
（1）证明：当0≤x≤1时，
（i）函数f（x）的最大值为|2a﹣b|+a；
（ii）f（x）+|2a﹣b|+a≥0；
（2）若﹣1≤f（x）≤1对x∈[0，1]恒成立，求a+b的取值范围．
【答案】
（1）证明：（ⅰ）f′（x）=12a（x2﹣ 
）
当b≤0时，f′（x）＞0，在0≤x≤1上恒成立，此时最大值为：f（1）=|2a﹣b|﹢a；
当b＞0时，在0≤x≤1上的正负性不能判断，f'（x）在区间[0，1]先负后可能正，f（x）图象在[0，1]区间内是凹下去的，所以最大值正好取在区间的端点，此时最大值为：f（x）max=max{f（0），f（1）}=|2a﹣b|﹢a；
综上所述：函数在0≤x≤1上的最大值为|2a﹣b|﹢a；
（ⅱ） 要证f（x）+|2a﹣b|+a≥0，即证g（x）=﹣f（x）≤|2a﹣b|﹢a．
亦即证g（x）在0≤x≤1上的最大值小于（或等于）|2a﹣b|﹢a，
∵g（x）=﹣4ax3+2bx+a﹣b，∴令g′（x）=﹣12ax2+2b=0，
当b≤0时， 
；g′（x）＜0在0≤x≤1上恒成立，
此时g（x）的最大值为：g（0）=a﹣b＜3a﹣b=|2a﹣b|﹢a；
当b＞0时，g′（x）在0≤x≤1上的正负性不能判断，
∴g（x）max=max{g（ 
），g（1）}={ 
}= 
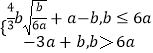
∴g（x）max≤|2a﹣b|﹢a；
综上所述：函数g（x）在0≤x≤1上的最大值小于（或等于）|2a﹣b|﹢a．
即f（x）+|2a﹣b|+a≥0在0≤x≤1上恒成立．
（2）解：由（1）知：函数在0≤x≤1上的最大值为|2a﹣b|﹢a，且函数在0≤x≤1上的最小值比﹣（|2a﹣b|﹢a）要大．
∵﹣1≤f（x）≤1对x∈[0，1]恒成立，
∴|2a﹣b|﹢a≤1．
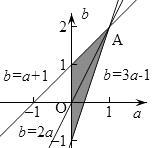
取b为纵轴，a为横轴，则可行域为： 
或 
，目标函数为z=a+b．
作图如右：
由图易得：a+b的取值范围为（﹣1，3]
【解析】（Ⅰ）（ⅰ）求导函数，再分类讨论：当b≤0时，f′（x）＞0在0≤x≤1上恒成立，此时最大值为：f（1）=|2a﹣b|﹢a；当b＞0时，在0≤x≤1上的正负性不能判断，此时最大值为：f（x）max=max{f（0），f（1）}=|2a﹣b|﹢a，由此可得结论；（ⅱ） 利用分析法，要证f（x）+|2a﹣b|+a≥0，即证g（x）=﹣f（x）≤|2a﹣b|﹢a．亦即证g（x）在0≤x≤1上的最大值小于（或等于）|2a﹣b|﹢a．（Ⅱ）由（Ⅰ）知：函数在0≤x≤1上的最大值为|2a﹣b|﹢a，且函数在0≤x≤1上的最小值比﹣（|2a﹣b|﹢a）要大．根据﹣1≤f（x）≤1对x∈[0，1]恒成立，可得|2a﹣b|﹢a≤1，从而利用线性规划知识，可求a+b的取值范围．
【考点精析】解答此题的关键在于理解函数的最大(小)值与导数的相关知识，掌握求函数
在
上的最大值与最小值的步骤：（1）求函数在
内的极值；（2）将函数的各极值与端点处的函数值
，
比较，其中最大的是一个最大值，最小的是最小值．
