题目内容
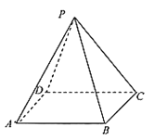
【题目】已知正四棱锥![]() 的底面边长和高都为2.现从该棱锥的5个顶点中随机选取3个点构成三角形,设随机变量
的底面边长和高都为2.现从该棱锥的5个顶点中随机选取3个点构成三角形,设随机变量![]() 表示所得三角形的面积.
表示所得三角形的面积.
(1)求概率![]() 的值;
的值;
(2)求随机变量![]() 的概率分布及其数学期望
的概率分布及其数学期望![]() .
.
【答案】(1)![]() (2)见解析
(2)见解析
【解析】
(1)由题意,分别得出“从5个顶点中随机选取3个点构成三角形”和“![]() ”所包含的基本事件个数,基本事件个数比即为所求概率;
”所包含的基本事件个数,基本事件个数比即为所求概率;
(2)先由题意得到![]() 的可能取值,求出对应的概率,进而可得到分布列,求出期望.
的可能取值,求出对应的概率,进而可得到分布列,求出期望.
解:(1)从5个顶点中随机选取3个点构成三角形,
共有![]() 种取法.其中
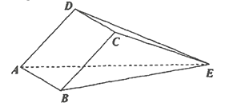
种取法.其中![]() 的三角形如
的三角形如![]() ,
,
这类三角形共有![]() 个.
个.
因此![]() .
.
(2)由题意,![]() 的可能取值为
的可能取值为![]() ,2,
,2,![]() .
.
其中![]() 的三角形是侧面,这类三角形共有4个;
的三角形是侧面,这类三角形共有4个;
其中![]() 的三角形有两个,
的三角形有两个,![]() 和
和![]() .
.
因此![]() ,
,![]() .
.
所以随机变量![]() 的概率分布列为:
的概率分布列为:
|
| 2 |
|
|
|
|
|
所求数学期望
![]() .
.

 优生乐园系列答案
优生乐园系列答案【题目】为了促进我国人口均衡发展,从2016年1月1日起,全国统一实施全面放开二孩政策,这也是为了重建大国人口观,重新认识人口价值、人口规律、人口问题,某研究机构为了了解人们对全面放开生育二孩政策的态度,随机调查了200人,得到的统计数据如下面的不完整的2×2列联表所示(单位:人):
支持生育二孩 | 不支持生育二孩 | 合计 | |
男性 | 30 | ||
女性 | 60 | 100 | |
合计 | 70 |
(1)完成2×2列联表,并求是否有90%的把握认为是否“支持生育二孩”与性别有关?
(2)现从样本中的女性中利用分层抽样的方法抽取5人,再从这5人中随机选出2人进行深层次的交流,求选出的2人中至少有1人“支持生育二孩”的概率.
参考公式: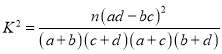 ,其中
,其中![]() .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
【题目】为迎接“五一国际劳动节”,某商场规定购买超过6000元商品的顾客可以参与抽奖活动现有甲品牌和乙品牌的扫地机器人作为奖品,从这两种品牌的扫地机器人中各随机抽取6台检测它们充满电后的工作时长相关数据见下表(工作时长单位:分)
机器序号 | 1 | 2 | 3 | 4 | 5 | 6 |
甲品牌工作时长/分 | 220 | 180 | 210 | 220 | 200 | 230 |
乙品牌工作时长/分 | 200 | 190 | 240 | 230 | 220 | 210 |
(1)根据所提供的数据,计算抽取的甲品牌的扫地机器人充满电后工作时长的平均数与方差;
(2)从乙品牌被抽取的6台扫地机器人中随机抽出3台扫地机器人,记抽出的扫地机器人充满电后工作时长不低于220分钟的台数为![]() ,求
,求![]() 的分布列与数学期望.
的分布列与数学期望.
【题目】在某外国语学校举行的![]() (高中生数学建模大赛)中,参与大赛的女生与男生人数之比为
(高中生数学建模大赛)中,参与大赛的女生与男生人数之比为![]() ,且成绩分布在
,且成绩分布在![]() ,分数在
,分数在![]() 以上(含
以上(含![]() )的同学获奖.按女生、男生用分层抽样的方法抽取
)的同学获奖.按女生、男生用分层抽样的方法抽取![]() 人的成绩作为样本,得到成绩的频率分布直方图如图所示.
人的成绩作为样本,得到成绩的频率分布直方图如图所示.
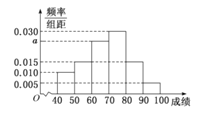
(Ⅰ)求![]() 的值,并计算所抽取样本的平均值
的值,并计算所抽取样本的平均值![]() (同一组中的数据用该组区间的中点值作代表);
(同一组中的数据用该组区间的中点值作代表);
(Ⅱ)填写下面的![]() 列联表,并判断在犯错误的概率不超过
列联表,并判断在犯错误的概率不超过![]() 的前提下能否认为“获奖与女生、男生有关”.
的前提下能否认为“获奖与女生、男生有关”.
女生 | 男生 | 总计 | |
获奖 |
| ||
不获奖 | |||
总计 |
| ||
附表及公式:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
其中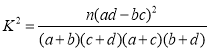 ,
,![]() .
.
【题目】为了丰富学生的课外文化生活,某中学积极探索开展课外文体活动的新途径及新形式,取得了良好的效果.为了调查学生的学习积极性与参加文体活动是否有关,学校对200名学生做了问卷调查,列联表如下:
参加文体活动 | 不参加文体活动 | 合计 | |
学习积极性高 | 80 | ||
学习积极性不高 | 60 | ||
合计 | 200 |
已知在全部200人中随机抽取1人,抽到学习积极性不高的学生的概率为![]() .
.
(1)请将上面的列联表补充完整;
(2)是否有99.9%的把握认为学习积极性高与参加文体活动有关?请说明你的理由;
(3)若从不参加文体活动的同学中按照分层抽样的方法选取5人,再从所选出的5人中随机选取2人,求至少有1人学习积极性不高的概率.
附:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
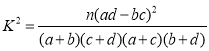 ,其中
,其中![]() .
.