题目内容
已知函数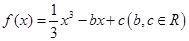
(1)若函数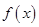 在点
在点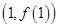 处的切线方程为
处的切线方程为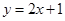 ,求
,求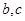 的值;
的值;
(2)若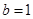 ,函数
,函数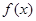 在区间
在区间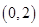 内有唯一零点,求
内有唯一零点,求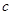 的取值范围;
的取值范围;
(3)若对任意的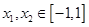 ,均有
,均有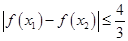 ,求
,求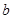 的取值范围.
的取值范围.
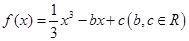
(1)若函数
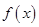 在点
在点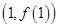 处的切线方程为
处的切线方程为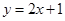 ,求
,求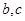 的值;
的值;(2)若
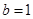 ,函数
,函数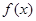 在区间
在区间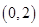 内有唯一零点,求
内有唯一零点,求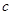 的取值范围;
的取值范围;(3)若对任意的
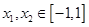 ,均有
,均有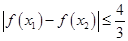 ,求
,求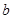 的取值范围.
的取值范围.(1)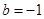 ,
,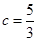 ;(2)
;(2)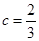 或
或 ;(3)
;(3)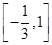 .
.
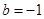 ,
,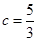 ;(2)
;(2)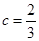 或
或 ;(3)
;(3)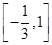 .
.试题分析:本题考查导数的运算,利用导数求切线方程、判断函数的单调性、求函数的最值等基础知识,考查函数思想、分类讨论思想,考查综合分析和解决问题的能力.第一问,利用导数求切线方程,先求导,将切点的横坐标代入到导数中,得到切线的斜率,再求
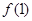 即切点的纵坐标,直接利用点斜式写出切线方程;第二问,先将
即切点的纵坐标,直接利用点斜式写出切线方程;第二问,先将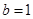 代入得到
代入得到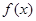 解析式,求导数,判断函数的单调性,因为
解析式,求导数,判断函数的单调性,因为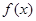 在
在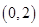 有唯一的零点,所以
有唯一的零点,所以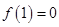 或
或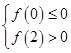 ,所以解得
,所以解得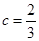 或
或 ;第三问,属于恒成立问题,通过分析题意,可以转化为
;第三问,属于恒成立问题,通过分析题意,可以转化为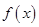 在
在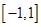 上的最大值与最小值之差
上的最大值与最小值之差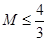 ,因为
,因为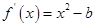 ,所以讨论
,所以讨论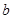 的正负来判断
的正负来判断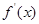 的正负,当
的正负,当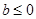 时,
时,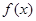 为单调函数,所以
为单调函数,所以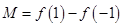 ,当
,当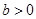 时,需列表判断函数的单调性和极值来决定最值的位置,这种情况中还需要讨论
时,需列表判断函数的单调性和极值来决定最值的位置,这种情况中还需要讨论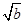 与1的大小.
与1的大小.试题解析:(1)
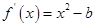 ,所以
,所以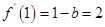 ,得
,得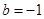 . 2分
. 2分又
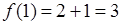 ,所以
,所以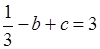 ,得
,得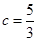 . 3分
. 3分(2) 因为
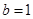 所以
所以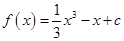 ,
,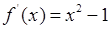 . 4分
. 4分当
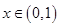 时,
时,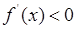 ,当
,当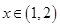 时,
时,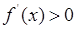
所以
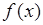 在
在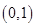 上单调递减,在
上单调递减,在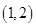 上单调递增 5分
上单调递增 5分又
 ,可知
,可知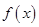 在区间
在区间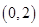 内有唯一零点等价于
内有唯一零点等价于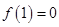 或
或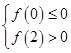 , . 7分
, . 7分得
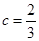 或
或 . 8分
. 8分(3)若对任意的
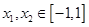 ,均有
,均有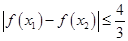 ,等价于
,等价于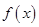 在
在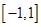 上的最大值与最小值之差
上的最大值与最小值之差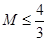 10分
10分(ⅰ) 当
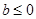 时,在
时,在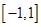 上
上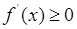 ,
,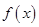 在
在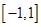 上单调递增,
上单调递增,由
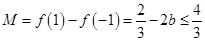 ,得
,得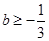 ,
,所以
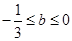 9分
9分(ⅱ)当
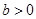 时,由
时,由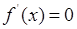 得
得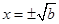

由
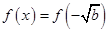 得
得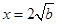 或
或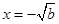
所以
 ,同理
,同理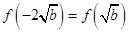 . 10分
. 10分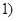 当
当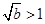 ,即
,即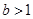 时,
时,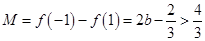 ,与题设矛盾; 11分
,与题设矛盾; 11分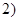 当
当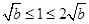 ,即
,即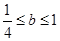 时,
时,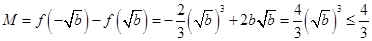 恒成立; 12分
恒成立; 12分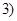 当
当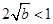 ,即
,即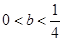 时,
时,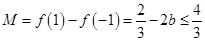 恒成立; 13分
恒成立; 13分综上所述,
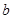 的取值范围为
的取值范围为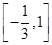 . 14分
. 14分
练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案
相关题目
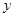 (单位:千套)与销售价格
(单位:千套)与销售价格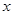 (单位:元/套)满足的关系式
(单位:元/套)满足的关系式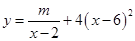 ,其中
,其中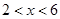 ,
,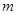 为常数.已知销售价格为4元/套时,每日可售出套题21千套.
为常数.已知销售价格为4元/套时,每日可售出套题21千套.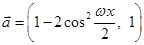 ,
,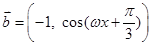 ,
,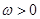 ,点A、B为函数
,点A、B为函数 的相邻两个零点,AB=π.
的相邻两个零点,AB=π. 的值;
的值; ,
, ,求
,求 的值;
的值; 在区间
在区间 上的单调递减区间.
上的单调递减区间.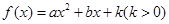 在
在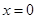 处取得极值,且曲线
处取得极值,且曲线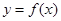 在点
在点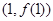 处的切线垂直于直线
处的切线垂直于直线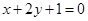 .
.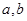 的值;
的值;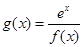 ,讨论
,讨论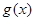 的单调性.
的单调性.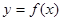 在
在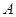 ,
, 两点间的平均变化率是( )
两点间的平均变化率是( )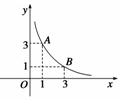
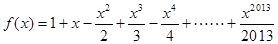 ,
,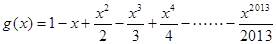 ,设函数
,设函数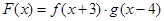 ,且函数
,且函数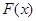 的零点均在区间
的零点均在区间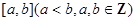 内,则
内,则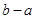 的最小值为( )
的最小值为( )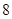
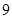
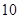
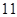
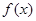 是定义域为
是定义域为 的奇函数,且
的奇函数,且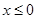 时,
时, ,则函数
,则函数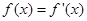 的实数根
的实数根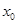 叫做函数
叫做函数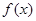 的“新驻点”,若函数
的“新驻点”,若函数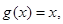
 的“新驻点”分别为
的“新驻点”分别为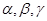 ,则
,则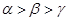
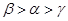
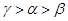
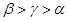
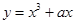 在原点处的切线方程是
在原点处的切线方程是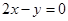 ,则实数
,则实数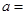 .
.