题目内容
18.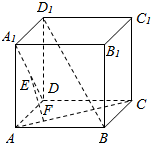 如图,在正方体ABCD-A1B1C1D1中,点E,F分别在A1D,AC上,且EF⊥A1D,EF⊥AC.求证:EF∥BD1.
如图,在正方体ABCD-A1B1C1D1中,点E,F分别在A1D,AC上,且EF⊥A1D,EF⊥AC.求证:EF∥BD1.
分析 连结A1C1,由已知条件推导出EF⊥平面A1C1D,BD1⊥平面A1C1D,由此利用线面垂直的性质能证明EF∥BD1.
解答  证明:连结A1C1,由于AC∥A1C1,EF⊥AC,
证明:连结A1C1,由于AC∥A1C1,EF⊥AC,
∴EF⊥A1C1,
又EF⊥A1D,A1D∩A1C1=A1,
∴EF⊥平面A1C1D,①
∵BB1⊥平面A1B1C1D1,A1C1?平面A1B1C1D1,
∴BB1⊥A1C1,
又A1B1C1D1为正方体,
∴A1C1⊥B1D1,
∵BB1∩B1D1=B1,
∴A1C1⊥平面BB1D1D,
而BD1?平面BB1D1D,
∴BD1⊥A1C1,
同理,DC1⊥BD1,DC1∩A1C1=C1,
∴BD1⊥平面A1C1D,②
由①②,得EF∥BD1.
点评 本题考查两条直线平行的证明,是中档题,解题时要认真审题,注意空间中线线、线面、面面间的位置关系的合理运用.

练习册系列答案
相关题目
8.函数的定义域是$y=(x-1)^{0}+\sqrt{lo{g}_{\frac{2}{3}}(3x-2)}$( )
| A. | [$\frac{2}{3},1$] | B. | ($\frac{2}{3},1$] | C. | [$\frac{2}{3},1$) | D. | ($\frac{2}{3},1$) |
7.函数f(x)=ln(sin2x-cos2x)的定义域是( )
| A. | 2kπ-$\frac{3π}{4}$<x<2kπ+$\frac{π}{4}$,k∈Z | B. | 2kπ+$\frac{π}{4}$<x<2k$π+\frac{5π}{4}$,k∈Z | ||
| C. | k$π-\frac{π}{4}$<x<k$π+\frac{π}{4}$,k∈Z | D. | k$π+\frac{π}{4}$<x<k$π+\frac{3π}{4}$,k∈Z |
 如图所示的数阵是由非零自然数连续排列构成的,其中第n行中有n个数,则第n行所有数的和是$\frac{1}{2}$n(n2+1).
如图所示的数阵是由非零自然数连续排列构成的,其中第n行中有n个数,则第n行所有数的和是$\frac{1}{2}$n(n2+1).