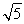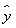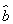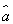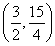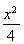题目内容
样本(x1，x2，…，xn)的平均数为x，样本(y1，y2，…，ym)的平均数为y(x≠y)．若样本(x1，x2，…，xn，y1，y2，…，ym)的平均数z＝αx＋(1－α)y，其中0<α<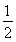
，则n，m的大小关系为( )
A．n<m B．n>m C．n＝m D．不能确定
A
【解析】由题意知，样本(x1，…，xn，y1，…，ym)的平均数为z＝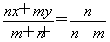
x＋
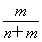y，且z＝αx＋(1－α)y，所以α＝
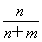，1－α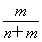＝.又因为0<α<
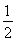，所以0<<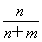
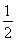，解得n<m.故选A.
练习册系列答案
阅读快车系列答案
相关题目
某班主任对全班30名男生进行了作业量多少的调查，数据如下表：
| 认为作业多 | 认为作业不多 | 总数 |
喜欢玩电脑游戏 | 12 | 8 | 20 |
不喜欢玩电脑游戏 | 2 | 8 | 10 |
总数 | 14 | 16 | 30 |
该班主任据此推断认为男生喜欢玩电脑游戏与作业量的多少有关，这种推断犯错误的概率不超过________．
附：K2＝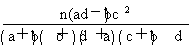
P(K2>k) | 0.050 | 0.010 | 0.001 |
k | 3.841 | 6.625 | 10.828 |
