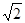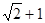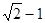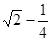题目内容
第(1)小题满分4分,第(2)小题满分6分,第(3)小题满分6分.
已知点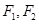 为双曲线
为双曲线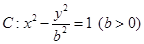 的左、右焦点,过
的左、右焦点,过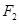 作垂直于
作垂直于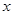 轴的直线,在
轴的直线,在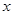 轴上方交双曲线于点
轴上方交双曲线于点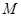 ,且
,且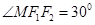 ,圆
,圆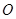 的方程为
的方程为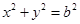 .
.
(1)求双曲线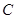 的方程;
的方程;
(2)过圆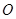 上任意一点
上任意一点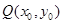 作切线
作切线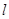 交双曲线
交双曲线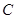 于
于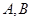 两个不同点,
两个不同点,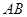 中点为
中点为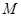 ,
,
求证: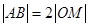 ;
;
(3)过双曲线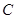 上一点
上一点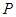 作两条渐近线的垂线,垂足分别是
作两条渐近线的垂线,垂足分别是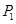 和
和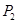 ,求
,求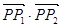 的值
的值
已知点
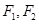 为双曲线
为双曲线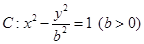 的左、右焦点,过
的左、右焦点,过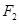 作垂直于
作垂直于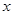 轴的直线,在
轴的直线,在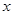 轴上方交双曲线于点
轴上方交双曲线于点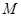 ,且
,且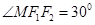 ,圆
,圆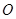 的方程为
的方程为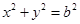 .
. (1)求双曲线
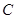 的方程;
的方程;(2)过圆
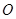 上任意一点
上任意一点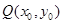 作切线
作切线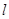 交双曲线
交双曲线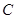 于
于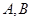 两个不同点,
两个不同点,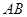 中点为
中点为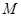 ,
,求证:
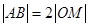 ;
;(3)过双曲线
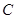 上一点
上一点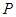 作两条渐近线的垂线,垂足分别是
作两条渐近线的垂线,垂足分别是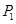 和
和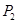 ,求
,求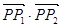 的值
的值(1)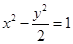 ;(2)见解析;(3)
;(2)见解析;(3)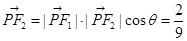
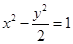 ;(2)见解析;(3)
;(2)见解析;(3)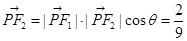
本试题主要考查了双曲线的运用。
解:(1)设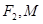 的坐标分别为
的坐标分别为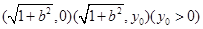 ----------------1分
----------------1分
因为点M在双曲线C上,所以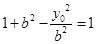 ,即
,即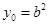 ,所以
,所以 ------2分
------2分
在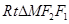
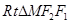 中,
中, ,
,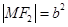 ,所以
,所以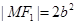 -------3分
-------3分
由双曲线的定义可知: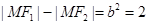
故双曲线C的方程为: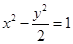 -------------------4分
-------------------4分
(2)①当切线l的斜率存在
设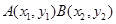 ,切线
,切线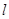 的方程为:
的方程为: 
代入双曲线C中,化简得: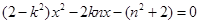
所以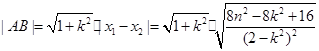 -------------------6分
-------------------6分
因为直线l与圆O相切,所以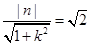 ,代入上式,得
,代入上式,得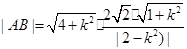 -----------7分
-----------7分
设点M的坐标为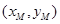 ,则
,则
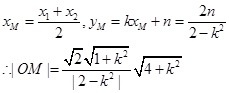
所以-------------------8分
即|AB|=2|OM|成立
②当切线l的斜率不存在时,
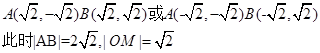 ,
,
即|AB|=2|OM|成立-------------------10分
(3)由条件可知:两条渐近线分别为
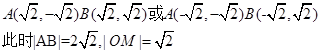
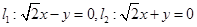 ------11分
------11分
设双曲线C上的点P(x0,y0),
则点P到两条渐近线的距离分别为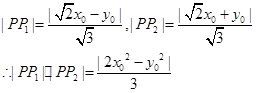 --------------13分
--------------13分
因为P(x0,y0),在双曲线C: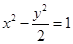 上,所以
上,所以
故 -------------------14分
-------------------14分
设 -------------15分
-------------15分
-----16分
解:(1)设
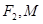 的坐标分别为
的坐标分别为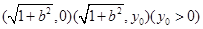 ----------------1分
----------------1分因为点M在双曲线C上,所以
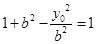 ,即
,即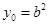 ,所以
,所以 ------2分
------2分在
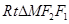
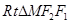 中,
中, ,
,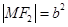 ,所以
,所以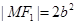 -------3分
-------3分由双曲线的定义可知:
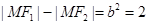
故双曲线C的方程为:
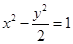 -------------------4分
-------------------4分(2)①当切线l的斜率存在
设
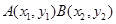 ,切线
,切线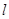 的方程为:
的方程为: 
代入双曲线C中,化简得:
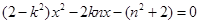
所以
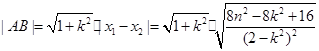 -------------------6分
-------------------6分因为直线l与圆O相切,所以
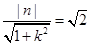 ,代入上式,得
,代入上式,得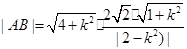 -----------7分
-----------7分设点M的坐标为
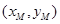 ,则
,则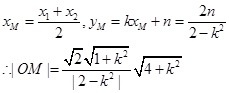
所以-------------------8分
即|AB|=2|OM|成立
②当切线l的斜率不存在时,
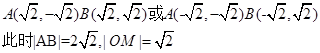 ,
,即|AB|=2|OM|成立-------------------10分
(3)由条件可知:两条渐近线分别为
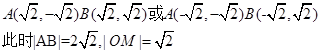
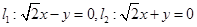 ------11分
------11分设双曲线C上的点P(x0,y0),
则点P到两条渐近线的距离分别为
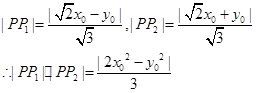 --------------13分
--------------13分因为P(x0,y0),在双曲线C:
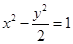 上,所以
上,所以
故
 -------------------14分
-------------------14分设
 -------------15分
-------------15分-----16分

练习册系列答案
相关题目
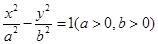 的渐近线与抛物线
的渐近线与抛物线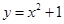 相切,则该双曲线的离心率为
相切,则该双曲线的离心率为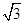
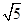
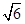
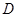 是由双曲线
是由双曲线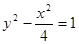 的两条渐近线和椭圆
的两条渐近线和椭圆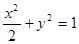 的右准线所围成的三角形(含边界与内部).若点
的右准线所围成的三角形(含边界与内部).若点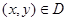 ,则目标函数
,则目标函数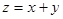 的最大值为 ( )
的最大值为 ( )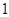
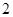
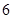
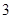
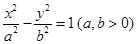 右支上一点,
右支上一点,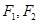 为双曲线的左、右焦点,O为坐标原点,若
为双曲线的左、右焦点,O为坐标原点,若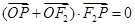 ,且
,且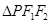 的面积为
的面积为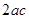 (
(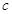 为双曲线的半焦距),则双曲线的离心率为( )
为双曲线的半焦距),则双曲线的离心率为( )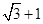
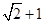
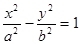 的离心率为
的离心率为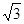 ,则它的渐近线方程是 ( )
,则它的渐近线方程是 ( )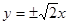
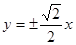
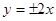
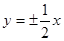
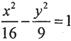 的左、右焦点,P为双曲线右支上一点,I是
的左、右焦点,P为双曲线右支上一点,I是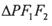 的内心,且
的内心,且 ,则
,则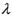 =
=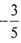
 的离心率为
的离心率为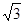 ,则椭圆
,则椭圆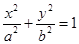 的离心率为( )
的离心率为( )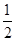
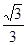
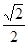
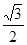
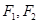 是双曲线
是双曲线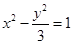 的两个焦点,点
的两个焦点,点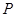 是双曲线上的点,并且
是双曲线上的点,并且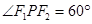 ,则
,则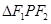 的面积为____.
的面积为____.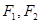 是双曲线的两个焦点,
是双曲线的两个焦点,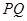 是经过
是经过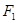 且垂直于实轴的弦,若
且垂直于实轴的弦,若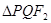 是等腰直角三角形,则双曲线的离心率为 ( )
是等腰直角三角形,则双曲线的离心率为 ( )