题目内容
求数列1+1,
+4,
+7,
+10,…,
+(3n-2),…的前n项和.
| 1 |
| a |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| an-1 |
考点:数列的求和
专题:等差数列与等比数列
分析:对a分类讨论,分组分别利用等比数列与等差数列的前n项和公式即可得出.
解答:
解:Sn=1+1+
+4+
+7+
+10+…+
+(3n-2)
=1+
+
+
+…+
+1+4+…+(3n-2).
当a=1时,Sn=n+
=
.
当a≠1时,Sn=
+
=
+
.
| 1 |
| a |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| an-1 |
=1+
| 1 |
| a |
| 1 |
| a2 |
| 1 |
| a3 |
| 1 |
| an-1 |
当a=1时,Sn=n+
| n(1+3n-2) |
| 2 |
| 3n2+n |
| 2 |
当a≠1时,Sn=
1-
| ||
1-
|
| n(1+3n-2) |
| 2 |
| an-1 |
| an-an-1 |
| 3n2-n |
| 2 |
点评:本题考查了等比数列与等差数列的前n项和公式,考查了分类讨论的思想方法,属于基础题.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
在四边形ABCD中,若
=
+
,则四边形ABCD的形状一定是( )
| AC |
| AB |
| AD |
| A、平行四边形 | B、菱形 |
| C、矩形 | D、正方形 |
设2b是1-a和1+a的等比中项,则a+4b的最大值为( )
| A、1 | ||||
| B、3 | ||||
C、
| ||||
D、
|
已知
,则
的最大值为( )
|
| y-2 |
| x-3 |
| A、2 | ||
B、
| ||
| C、0 | ||
D、
|
条件甲:复数z为纯虚数,条件乙:z+
=0,那么甲是乙的( )
. |
| z |
| A、必要非充分条件 |
| B、充分非必要条件 |
| C、充要条件 |
| D、既非充分又非必要条件 |
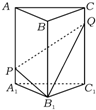 在如图所示,直三棱柱ABC-A1B1C1中,P,Q分别是侧棱AA1,CC1上的点,且A1P=CQ,则四棱锥B1-A1PQC1的体积与多面体ABC-PB1Q的体积比值为
在如图所示,直三棱柱ABC-A1B1C1中,P,Q分别是侧棱AA1,CC1上的点,且A1P=CQ,则四棱锥B1-A1PQC1的体积与多面体ABC-PB1Q的体积比值为