题目内容
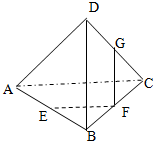
如图，三棱锥D-ABC中，E、F、G分别是AB、BC、CD的中点，共有 对线面平行．
考点：直线与平面平行的判定
专题：空间位置关系与距离
分析：由三棱锥D-ABC中，E、F、G分别是AB、BC、CD的中点，得GF∥BD，FE∥AC，GE∥AD，由此能求出共在3对线面平行．
解答：
解：∵三棱锥D-ABC中，E、F、G分别是AB、BC、CD的中点，
∴GF∥BD，FE∥AC，
又GF不包含于平面ABD，BD?平面ABD，∴GF∥平面ABD，
EF不包含于平面ADC，AC?平面ABD，∴EF∥平面ADC，
∴共在2对线面平行．
故答案为：2．
∴GF∥BD，FE∥AC，
又GF不包含于平面ABD，BD?平面ABD，∴GF∥平面ABD，
EF不包含于平面ADC，AC?平面ABD，∴EF∥平面ADC，
∴共在2对线面平行．
故答案为：2．
点评：本题考查三棱锥中线面平行的对数的求法，是中档题，解题时要认真审题，注意空间思维能力的培养．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
如图，在一条河流的上、下游分别有甲、乙两家化工厂，其中甲厂每天向河道内排放污水2万m3，每天流过甲厂的河水流量是500万m3（含甲厂排放的污水）；乙厂每天向河道内排放污水1.4万m3，每天流过乙厂的河水流量是700万m3（含乙厂排放的污水）．由于两厂之间有一条支流的作用，使得甲厂排放的污水在流到乙厂时，有20%可自然净化．假设工厂排放的污水能迅速与河水混合，且甲厂上游及支流均无污水排放．
如图，在椭圆