题目内容
【题目】已知函数![]() 具有如下性质:在
具有如下性质:在![]() 上是减函数,在
上是减函数,在![]() 上是增函数.
上是增函数.
(1)若函数![]() 的值域为
的值域为![]() ,求b的值;
,求b的值;
(2)已知函数![]() ,
,![]() ,求函数
,求函数![]() 的单调区间和值域;
的单调区间和值域;
(3)对于(2)中的函数![]() 和函数
和函数![]() ,若对任意
,若对任意![]() ,总存在
,总存在![]() ,使得
,使得![]() 成立,求实数c的值.
成立,求实数c的值.
【答案】(1)![]() (2)
(2)![]() 在
在![]() 上递减,在
上递减,在![]() 上递增;值域为
上递增;值域为![]() (3)
(3)![]()
【解析】
(1)由所给函数![]() 知,即可得出对于函数
知,即可得出对于函数![]() ,当
,当![]() 时取得最小值
时取得最小值![]() ,解出即可.
,解出即可.
(2)设![]() ,
,![]() ,
,![]() .由所给函数
.由所给函数![]() 性质知:
性质知:![]() 在
在![]() 单调递减,在
单调递减,在![]() 单调递增.进而取得最值.
单调递增.进而取得最值.
(3)![]() 在
在![]() 单调递减,可得
单调递减,可得![]() .对任意
.对任意![]() ,总存在
,总存在![]() ,使得
,使得![]() 成立,
成立,![]() ,解出即可.
,解出即可.
解:(1)由条件知![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
所以当![]() 时,则
时,则![]() ,所以
,所以![]() .
.
(2)令![]() ,则
,则![]() ,
,
所以![]() ,
,
由条件知![]() 在
在![]() 上递减,在
上递减,在![]() 上递增,
上递增,
而![]() 在
在![]() 上递增,
上递增,
根据复合函数单调性知![]() 在
在![]() 即
即![]() 上递减,
上递减,
在![]() 即
即![]() 上递增,
上递增,
所以![]() 在
在![]() 上递减,在
上递减,在![]() 上递增;
上递增;
根据![]() 的单调性知,
的单调性知,
当![]() 时,
时,![]() ,
,
当![]() 时,
时,![]() ,所以值域为
,所以值域为![]() .
.
(3)![]() 的值域为
的值域为![]() ,
,
对任意![]() ,总存在
,总存在![]() ,使得
,使得![]() 成立
成立
由题意知![]() 的值域为
的值域为![]() 的值域的子集,
的值域的子集,
所以![]()
所以![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
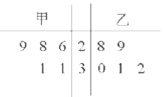
小学生10分钟应用题系列答案【题目】某地区高考实行新方案,规定:语文、数学和英语是考生的必考科目,考生还须从物理、化学、生物、历史、地理和政治六个科目中选取三个科目作为选考科目,若一名学生从六个科目中选出了三个科目作为选考科目,则称该学生的选考方案确定;否则,称该学生选考方案待确定.例如,学生甲选择“物理、化学和生物”三个选考科目,则学生甲的选考方案确定,“物理、化学和生物”为其选考方案.
某学校为了了解高一年级420名学生选考科目的意向,随机选取30名学生进行了一次调查,统计选考科目人数如下表:
性别 | 选考方案确定情况 | 物理 | 化学 | 生物 | 历史 | 地理 | 政治 |
男生 | 选考方案确定的有8人 | 8 | 8 | 4 | 2 | 1 | 1 |
选考方案待确定的有6人 | 4 | 3 | 0 | 1 | 0 | 0 | |
女生 | 选考方案确定的有10人 | 8 | 9 | 6 | 3 | 3 | 1 |
选考方案待确定的有6人 | 5 | 4 | 1 | 0 | 0 | 1 |
(Ⅰ)估计该学校高一年级选考方案确定的学生中选考生物的学生有多少人?
(Ⅱ)假设男生、女生选择选考科目是相互独立的.从选考方案确定的8位男生随机选出1人,从选考方案确定的10位女生中随机选出1人,试求该男生和该女生的选考方案中都含有历史科目的概率;
(Ⅲ)从选考方案确定的8名男生随机选出2名,设随机变量两名男生选考方案相同时![]() ,两名男生选考方案不同时
,两名男生选考方案不同时![]() ,求
,求![]() 的分布列及数学期望
的分布列及数学期望![]() .
.