题目内容
【题目】已知函数f(x)= ![]() +b(a,b∈R)的图象在点(1,f(1))处的切线方程为y=x﹣1.
+b(a,b∈R)的图象在点(1,f(1))处的切线方程为y=x﹣1.
(1)求实数a,b的值及函数f(x)的单调区间.
(2)当f(x1)=f(x2)(x1≠x2)时,比较x1+x2与2e(e为自然对数的底数)的大小.
【答案】
(1)解:f′(x)= ![]() ,
,
∵函数f(x)图象在点(1,f(1))处的切线方程为y=x﹣1,
∴ 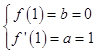 ,
,
∴f(x)= ![]() ,定义域为(0,+∞),
,定义域为(0,+∞),
∴f′(x)= ![]()
∴x∈(0,e),f′(x)>0,x∈(e,+∞),f′(x)<0,
∴f(x)的单调增区间是(0,e),单调减区间是(e,+∞)
(2)解:当f(x1)=f(x2)(x1≠x2)时,x1+x2>2e,
下面证明结论,
当x>e时,f(x)= ![]() >0,由(1)可知f(x)的单调增区间是(0,e),单调减区间是(e,+∞),
>0,由(1)可知f(x)的单调增区间是(0,e),单调减区间是(e,+∞),
又f(1)=0,
∴若f(x1)=f(x2)(x1≠x2),则x1,x2都大于1,且必有一个小于e,一个大于e,
设1<x1<e<x2,
当x2≥2e时,显然x1+x2>2e,
当e<x2<2e时,
∴f(x1)﹣f(2e﹣x2)=f(x2)﹣f(2e﹣x2)= ![]() ﹣
﹣ ![]() ,
,
设g(x)= ![]() ﹣
﹣ ![]() ,e<x<2e,
,e<x<2e,
∴g′(x)= ![]() {4e(e﹣x)(1﹣lnx)+x2[(2﹣ln(﹣(x﹣e)2+e2]},
{4e(e﹣x)(1﹣lnx)+x2[(2﹣ln(﹣(x﹣e)2+e2]},
∵e<x<2e,
∴0<﹣(x﹣e)2+e2<e2,
∴2﹣ln(﹣(x﹣e)2+e2>0
∵4e(e﹣x)(1﹣lnx)>0,
∴g′(x)>0,
∴g(x)在(e,2e)上单调递增,
∴g(x)>g(e)=0,
∴f(x1)>f(2e﹣x2),
∵1<x1<e<x2,
∴0<2e﹣x2<e,
∵f(x)在(0,e)上单调递增,
∴x1>2e﹣x2,
∴x1+x2>2e,
综上所述,当f(x1)=f(x2)(x1≠x2)时,x1+x2>2e
【解析】(1)根据导数几何意义即可求出a,b的值,根据导数和函数的单调性的关系即可求出,(2)当f(x1)=f(x2)(x1≠x2)时,x1+x2>2e,设1<x1<e<x2,当x2≥2e时,显然x1+x2>2e,当e<x2<2e时,构造函数,根据函数的单调性即可证明
【考点精析】根据题目的已知条件,利用利用导数研究函数的单调性的相关知识可以得到问题的答案,需要掌握一般的,函数的单调性与其导数的正负有如下关系: 在某个区间![]() 内,(1)如果
内,(1)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递增;(2)如果
在这个区间单调递增;(2)如果![]() ,那么函数
,那么函数![]() 在这个区间单调递减.
在这个区间单调递减.

【题目】已知某产品的广告费用x(单位:万元)与销售额y(单位:万元)具有线性关系关系,其统计数据如下表:
x | 3 | 4 | 5 | 6 |
y | 25 | 30 | 40 | 45 |
由上表可得线性回归方程 ![]() =
= ![]() x+
x+ ![]() ,据此模型预报广告费用为8万元时的销售额是( )
,据此模型预报广告费用为8万元时的销售额是( )
附: ![]() =
= 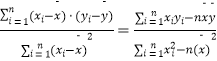 ;
; ![]() =
= ![]() ﹣
﹣ ![]() x.
x.
A.59.5
B.52.5
C.56
D.63.5
【题目】网购是当前民众购物的新方式,某公司为改进营销方式,随机调查了100名市民,统计其周平均网购的次数,并整理得到如下的频数分布直方图.这100名市民中,年龄不超过40岁的有65人将所抽样本中周平均网购次数不小于4次的市民称为网购迷,且已知其中有5名市民的年龄超过40岁. 
(1)根据已知条件完成下面的2×2列联表,能否在犯错误的概率不超过0.10的前提下认为网购迷与年龄不超过40岁有关?
网购迷 | 非网购迷 | 合计 | |
年龄不超过40岁 | |||
年龄超过40岁 | |||
合计 |
(2)若从网购迷中任意选取2名,求其中年龄丑啊过40岁的市民人数ξ的分布列与期望. 附: ![]() ;
;
P(K2≥k0) | 0.15 | 0.10 | 0.05 | 0.01 |
k0 | 2.072 | 2.706 | 3.841 | 6.635 |
【题目】某省高考改革新方案,不分文理科,高考成绩实行“3+3”的构成模式,第一个“3”是语文、数学、外语,每门满分150分,第二个“3”由考生在思想政治、历史、地理、物理、化学、生物6个科目中自主选择其中3个科目参加等级性考试,每门满分100分,高考录取成绩卷面总分满分750分.为了调查学生对物理、化学、生物的选考情况,将“某市某一届学生在物理、化学、生物三个科目中至少选考一科的学生”记作学生群体S,从学生群体S中随机抽取了50名学生进行调查,他们选考物理,化学,生物的科目数及人数统计如表:
选考物理、化学、生物的科目数 | 1 | 2 | 3 |
人数 | 5 | 25 | 20 |
(I)从所调查的50名学生中任选2名,求他们选考物理、化学、生物科目数量不相等的概率;
(II)从所调查的50名学生中任选2名,记X表示这2名学生选考物理、化学、生物的科目数量之差的绝对值,求随机变量X的分布列和数学期望;
(III)将频率视为概率,现从学生群体S中随机抽取4名学生,记其中恰好选考物理、化学、生物中的两科目的学生数记作Y,求事件“y≥2”的概率.

