题目内容
如图,正方形ABCD、ABEF的边长都是1,而且平面ABCD、ABEF互相垂直,点M在AC上移动,点N在BF上移动,若CM=BN=a(0<a<(1)求MN的长.
(2)当a为何值时,MN的长最小?
(3)当MN长最小时,求面MNA与面MNB所成的二面角α的大小.
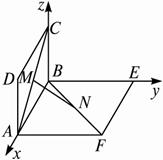
解析:为了求(1)中MN的长,根据图形特征,建立坐标系,写出![]() 的坐标形式,利用模公式求解.在(1)的基础上很容易求解(2),求解二面角时利用定义作出平面角,再用向量解决,也可用法向量求解.?
的坐标形式,利用模公式求解.在(1)的基础上很容易求解(2),求解二面角时利用定义作出平面角,再用向量解决,也可用法向量求解.?
解:(1)建立如图所示的空间直角坐标系,由题设得?
A(1,0,0),C(0,0,1),F(1,1,0).?
∵CM=BN=a,∴M(![]() ,0,1-
,0,1-![]() a),N(
a),N(![]() ,
,![]() ,0),
,0), ![]() =(0,
=(0,![]() ,
,![]() a-1).?
a-1).?
∴|![]() |=
|= (0<a<
(0<a<![]() ).?
).?
(2)由(1)知|![]() |=
|=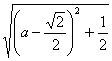 (0<a<
(0<a<![]() ).?
).?
当a=![]() 时,|
时,|![]() |取得最小值
|取得最小值![]() ,此时M、N分别是AC、BF的中点.?
,此时M、N分别是AC、BF的中点.?
(3)由(2)知,∵M、N分别为AC、BF的中点,?
∴AM=AN,BM=BN且M(![]() ,0,
,0,![]() ),N(
),N(![]() ,
,![]() ,0).?
,0).?
设MN的中点为O,则O(![]() ,
,![]() ,
,![]() )且OA⊥MN,OB⊥MN.?
)且OA⊥MN,OB⊥MN.?
∴∠AOB为二面角A-MN-B的平面角,![]() =(
=(![]() ,-
,-![]() ,-
,-![]() ),
),![]() =(-
=(-![]() ,-
,-![]() ,-
,-![]() ).
).
∴![]() ·
·![]() =
=![]() ,?
,?
|![]() |=|
|=|![]() |=
|=![]() .?
.?
∴cos∠AOB=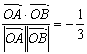 .?
.?
∴∠AOB=π-arccos![]() ,?
,?
即二面角α的大小为π-arccos![]() .
.

练习册系列答案
相关题目
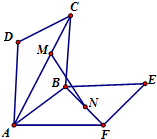 如图正方形ABCD,ABEF的边长都是1,而且平面ABCD,ABEF互相垂直.点M在AC上移动,点N在BF上移动,若CM=BN=a(0<a<
如图正方形ABCD,ABEF的边长都是1,而且平面ABCD,ABEF互相垂直.点M在AC上移动,点N在BF上移动,若CM=BN=a(0<a< 已知:如图正方形ABCD的边长为a,P,Q分别为AB,DA上的点,当△PAQ的周长为2a时,求∠PCQ.
已知:如图正方形ABCD的边长为a,P,Q分别为AB,DA上的点,当△PAQ的周长为2a时,求∠PCQ. 如图正方形ABCD和四边形ADEF所在的平面垂直,FA⊥AD,DE∥FA,且
如图正方形ABCD和四边形ADEF所在的平面垂直,FA⊥AD,DE∥FA,且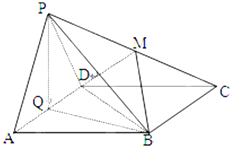 如图正方形ABCD所在平面与正△PAD所在平面互相垂直,M,Q分别为PC,AD的中点.
如图正方形ABCD所在平面与正△PAD所在平面互相垂直,M,Q分别为PC,AD的中点.