题目内容
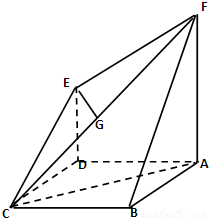
 如图正方形ABCD和四边形ADEF所在的平面垂直,FA⊥AD,DE∥FA,且AD=DE=
如图正方形ABCD和四边形ADEF所在的平面垂直,FA⊥AD,DE∥FA,且AD=DE=| 1 | 2 |
(1)求证:EG⊥平面ACF;
(2)求多面体ABCDEF的体积.
分析:(1)取AF中点H,连接GH,EH,由正方形ABCD和四边形ADEF所在的平面垂直,FA⊥AD,DE∥FA,且AD=DE=
AF=1,G是FC的中点,得到EH=AH=FH=CD=DE=1,EH⊥AF,ED⊥CD,GH∥AC,CE=EF=AC=
,GH=
,故EG⊥CF,再由EG2+GH2=EH2,知EG⊥GH,由此能够证明EG⊥平面ACF.
(2)连接FD,则多面体ABCDEF的体积:VABCDEF=VF-CDE+VF-ABCD,由VF-CDE=
×AD×S△CDE,VF-ABCD=
×AF×S正方形ABCD,能求出多面体ABCDEF的体积.
| 1 |
| 2 |
| 2 |
| ||
| 2 |
(2)连接FD,则多面体ABCDEF的体积:VABCDEF=VF-CDE+VF-ABCD,由VF-CDE=
| 1 |
| 3 |
| 1 |
| 3 |
解答: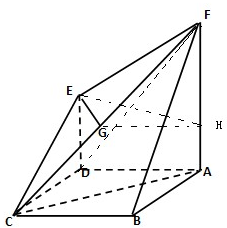 解:(1)取AF中点H,连接GH,EH,
解:(1)取AF中点H,连接GH,EH,
∵正方形ABCD和四边形ADEF所在的平面垂直,
FA⊥AD,DE∥FA,且AD=DE=
AF=1,G是FC的中点,
∴EH=AH=FH=CD=DE=1,EH⊥AF,ED⊥CD,GH∥AC,
∴CE=EF=AC=
=
,GH=
AC=
,
∴EG⊥CF,
∵FC=
=
=
,
∴EG=
=
=
,
∵EH=1,∴EG2+GH2=EH2,
∴EG⊥GH,
又∵CF∩GH=G,
∴EG⊥平面ACF.
(2)连接FD,则多面体ABCDEF的体积:
VABCDEF=VF-CDE+VF-ABCD
=
×AD×S△CDE+
×AF×S正方形ABCD
=
×1×
×1×1+
×2×12
=
+
=
.
 解:(1)取AF中点H,连接GH,EH,
解:(1)取AF中点H,连接GH,EH,∵正方形ABCD和四边形ADEF所在的平面垂直,
FA⊥AD,DE∥FA,且AD=DE=
| 1 |
| 2 |
∴EH=AH=FH=CD=DE=1,EH⊥AF,ED⊥CD,GH∥AC,
∴CE=EF=AC=
| 1+1 |
| 2 |
| 1 |
| 2 |
| ||
| 2 |
∴EG⊥CF,
∵FC=
| AF2+AC2 |
| 4+2 |
| 6 |
∴EG=
| EF2-FG2 |
2-
|
| ||
| 2 |
∵EH=1,∴EG2+GH2=EH2,
∴EG⊥GH,
又∵CF∩GH=G,
∴EG⊥平面ACF.
(2)连接FD,则多面体ABCDEF的体积:
VABCDEF=VF-CDE+VF-ABCD
=
| 1 |
| 3 |
| 1 |
| 3 |
=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
=
| 1 |
| 6 |
| 2 |
| 3 |
=
| 5 |
| 6 |
点评:本题考查直线与平面垂直的证明,考查多面体体积的求法,解题时要认真审题,仔细解答,注意中位线、勾股定理、等积法等知识点的合理运用.

练习册系列答案
相关题目
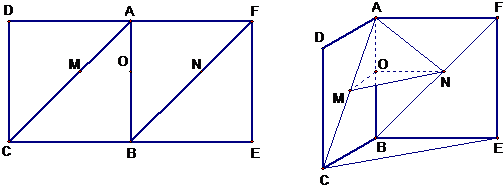
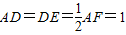 ,G是FC的中点.
,G是FC的中点.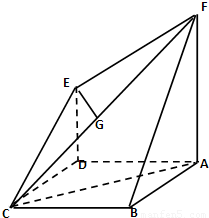
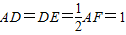 ,G是FC的中点.
,G是FC的中点.