题目内容
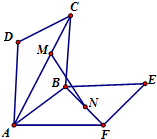 如图正方形ABCD,ABEF的边长都是1,而且平面ABCD,ABEF互相垂直.点M在AC上移动,点N在BF上移动,若CM=BN=a(0<a<
如图正方形ABCD,ABEF的边长都是1,而且平面ABCD,ABEF互相垂直.点M在AC上移动,点N在BF上移动,若CM=BN=a(0<a<| 2 |
(1)求MN的长;
(2)当a为何值时,MN的长最小.
分析:(1)作MP∥AB交BC于点,NQ∥AB交BE于点Q,连接PQ,易证MNQP是平行四边形,根据MN=PQ,即可求出MN的长;
(2)根据(1)将MN 关于a的函数进行配方即可求出MN的最小值,注意取最小值时a的取值即可得到结论.
(2)根据(1)将MN 关于a的函数进行配方即可求出MN的最小值,注意取最小值时a的取值即可得到结论.
解答:解:(1)作MP∥AB交BC于点P,NQ∥AB交BE于点Q,连接PQ,
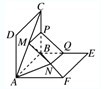
依题意可得MP∥NQ,且MP=NQ,即MNQP是平行四边形,∴MN=PQ
由已知CM=BN=a,CB=AB=BE=1
∴AC=BF=
,CP=BQ=
∴MN=PQ=
=
(0<a<
);
(2)由(1)MN=
(0<a<
)
∴当a=
时,MN的长最小为
即当M、N分别为AC、BF的中点时,MN的长最小,最小值为
.

依题意可得MP∥NQ,且MP=NQ,即MNQP是平行四边形,∴MN=PQ
由已知CM=BN=a,CB=AB=BE=1
∴AC=BF=
| 2 |
| a | ||
|
∴MN=PQ=
| (1-CP)2+BQ2 |
(a-
|
| 2 |
(2)由(1)MN=
(a-
|
| 2 |
∴当a=
| ||
| 2 |
| ||
| 2 |
即当M、N分别为AC、BF的中点时,MN的长最小,最小值为
| ||
| 2 |
点评:本题考查空间距离的计算,考查配方法的运用,考查学生的计算能力,属于中档题.

练习册系列答案
相关题目
 已知:如图正方形ABCD的边长为a,P,Q分别为AB,DA上的点,当△PAQ的周长为2a时,求∠PCQ.
已知:如图正方形ABCD的边长为a,P,Q分别为AB,DA上的点,当△PAQ的周长为2a时,求∠PCQ. 如图正方形ABCD和四边形ADEF所在的平面垂直,FA⊥AD,DE∥FA,且
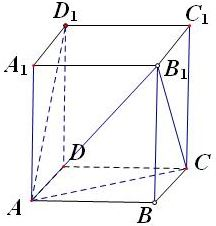
如图正方形ABCD和四边形ADEF所在的平面垂直,FA⊥AD,DE∥FA,且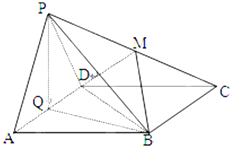 如图正方形ABCD所在平面与正△PAD所在平面互相垂直,M,Q分别为PC,AD的中点.
如图正方形ABCD所在平面与正△PAD所在平面互相垂直,M,Q分别为PC,AD的中点.