题目内容
已知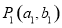 与
与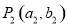 是直线
是直线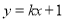 (
(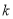 为常数)上两个不同的点,则关于
为常数)上两个不同的点,则关于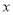 和
和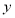 的方程组
的方程组 的解的情况是( )
的解的情况是( )
A.无论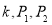 如何,总是无解 B.无论
如何,总是无解 B.无论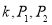 如何,总有唯一解
如何,总有唯一解
C.存在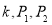 ,使之恰有两解 D.存在
,使之恰有两解 D.存在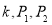 ,使之有无穷多解
,使之有无穷多解
练习册系列答案
 轻松暑假总复习系列答案
轻松暑假总复习系列答案
相关题目
题目内容
已知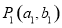 与
与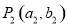 是直线
是直线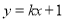 (
(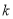 为常数)上两个不同的点,则关于
为常数)上两个不同的点,则关于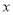 和
和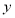 的方程组
的方程组 的解的情况是( )
的解的情况是( )
A.无论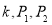 如何,总是无解 B.无论
如何,总是无解 B.无论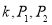 如何,总有唯一解
如何,总有唯一解
C.存在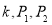 ,使之恰有两解 D.存在
,使之恰有两解 D.存在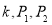 ,使之有无穷多解
,使之有无穷多解
 轻松暑假总复习系列答案
轻松暑假总复习系列答案