题目内容
10.求下列极限:(1)$\underset{lim}{n→∞}$(1$-\frac{1}{{2}^{2}}$)(1$-\frac{1}{{3}^{2}}$)…(1$-\frac{1}{{n}^{2}}$);
(2)$\underset{lim}{n→∞}$n2($\frac{k}{n}$$-\frac{1}{n+1}$$-\frac{1}{n+2}$-…$-\frac{1}{n+k}$).
分析 (1)(1$-\frac{1}{{2}^{2}}$)(1$-\frac{1}{{3}^{2}}$)…(1$-\frac{1}{{n}^{2}}$)=$\frac{2^2-1}{2^2}$•$\frac{3^2-1}{3^2}$•$\frac{4^2-1}{4^2}$…$\frac{n^2-1}{n^2}$=$\frac{n+1}{2n}$,再求极限;
(2)n2($\frac{k}{n}$$-\frac{1}{n+1}$$-\frac{1}{n+2}$-…$-\frac{1}{n+k}$)=n2•($\frac{1}{n(n+1)}$+$\frac{2}{n(n+2)}$+$\frac{3}{n(n+3)}$+…+$\frac{k}{n(n+k)}$),再求极限.
解答 解:(1)(1$-\frac{1}{{2}^{2}}$)(1$-\frac{1}{{3}^{2}}$)…(1$-\frac{1}{{n}^{2}}$)
=$\frac{2^2-1}{2^2}$•$\frac{3^2-1}{3^2}$•$\frac{4^2-1}{4^2}$…$\frac{n^2-1}{n^2}$
=$\frac{(1×3)•(2×4)•(3×5)…[(n-1)×(n+1)]}{2^2•3^2•4^2…n^2}$
=$\frac{1×2×n×(n+1)}{4n^2}$=$\frac{n+1}{2n}$,
所以,原式=$\underset{lim}{n→∞}$$\frac{n+1}{2n}$=$\frac{1}{2}$;
(2)$\frac{k}{n}$$-\frac{1}{n+1}$$-\frac{1}{n+2}$-…$-\frac{1}{n+k}$
=($\frac{1}{n}$$-\frac{1}{n+1}$)+($\frac{1}{n}$$-\frac{1}{n+2}$)+($\frac{1}{n}$-$\frac{1}{n+3}$)+…+($\frac{1}{n}$$-\frac{1}{n+k}$)
=$\frac{1}{n(n+1)}$+$\frac{2}{n(n+2)}$+$\frac{3}{n(n+3)}$+…+$\frac{k}{n(n+k)}$
所以,原式=$\underset{lim}{n→∞}$n2•($\frac{1}{n(n+1)}$+$\frac{2}{n(n+2)}$+$\frac{3}{n(n+3)}$+…+$\frac{k}{n(n+k)}$)
=1+2+3+…+k=$\frac{k(k+1)}{2}$.
点评 本题主要考查了数列极限的求法,采取了先对式子化简再求其极限的策略,属于中档题.

| A. | e${\;}^{{x}^{4}-{x}^{3}}$-1 | B. | cosx2-1 | C. | $\sqrt{1+{x}^{2}}$-1 | D. | tanx-sinx |

| A. | 2 | B. | $\frac{{\sqrt{6}+\sqrt{2}}}{2}$ | C. | $2+\sqrt{2}$ | D. | $\sqrt{2+\sqrt{2}}$ |
| A. | $[\frac{1}{4},\frac{1}{3})$ | B. | $(0,\frac{1}{2})$ | C. | $(0,\frac{1}{4}]$ | D. | $(\frac{1}{3},\frac{1}{2})$ |
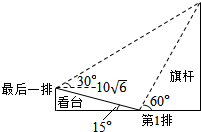 某校运动会开幕式上举行升旗仪式,在坡度为15°的看台上,同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°,第一排和最后一排的距离为10m(如图所示),则旗杆的高度为( )
某校运动会开幕式上举行升旗仪式,在坡度为15°的看台上,同一列上的第一排和最后一排测得旗杆顶部的仰角分别为60°和30°,第一排和最后一排的距离为10m(如图所示),则旗杆的高度为( )